合同条件について本気出して考えてみた~前編~ こんにちは。 和からの数学講師の岡本です。 今回は「三角形」の合同条件について本気出して考えてみたいと思います。 こうした図形に関する論理や証明といった話題合同数の問題 合同数の問題とは、どのような数が合同数になるかという問題である。これは数学上の未解決問題の一つである。 定義より明らかに、合同数は正の有理数である。また、辺の長さが (a, b, c) である直角三角形の面積が S であるとき、(k a, k b, k c) の面積は k 2 S であることから 中2数学「三角形の合同条件」条件の覚え方です。合同な図形の性質 合同な図形では、対応する線分の長さは、それぞれ等しい。 合同な図形では、対応する角の大きさは、それぞれ等しい。合同な表し方 ABCと EDFが合同であることを、記号≡を使っ

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
中2 数学合同条件
中2 数学合同条件- 三角形の合同条件 $2$ つの三角形について,それらが合同であるかどうかを確かめるためには,辺の長さや,角の大きさの情報がどの程度与えられていればよいでしょうか.三角形は $3$ の辺の長さと $3$ つの角の大きさという合計 $6$ つの基本的な情報をもっています.そして三角形のFdData 高校入試:中学数学2 年:三角形と四角形 仮定と結論,逆,合同条件/三角形の合同の証明/二等辺三角形の定理/ 二等辺三角形の性質を使った証明 /二等辺三角形になることを証明/正三角形/ 直角三角形/



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
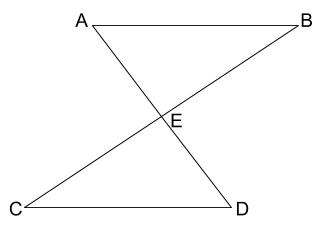
いろんな合同条件などがあり、ゴチャゴチャになりがちなので、まとめてみました! 学年 中学2年生, 単元 平行と合同の利用,三角形,四角形, キーワード 中学2年 数学 照明 合同条件 こんにちは、ウチダショウマです。 今日は、中学2年生で習う関門 「三角形の合同条件」 について、まずは図形の合同を確認し、次に合同条件を用いる証明問題を解き、またコラム的な内容も考察していきます。 コラム的な内容としては 目次4「作図を先に習う理由」目次2「3つの合同条件三角形が完全に決定される場合 1:三辺の長さ a, b, c a,b,c a,b,c が与えられた場合 余弦定理から角 A, B, C A,B,C A,B,C が求まります。 これは,「三辺の長さがそれぞれ等しい三角形は合同である」という事実と対応しています。 2:二辺の長さ
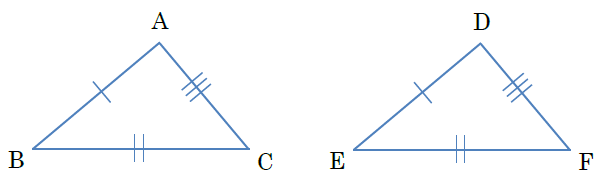
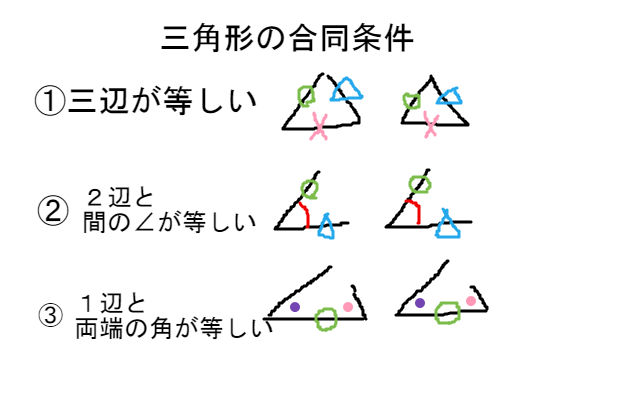
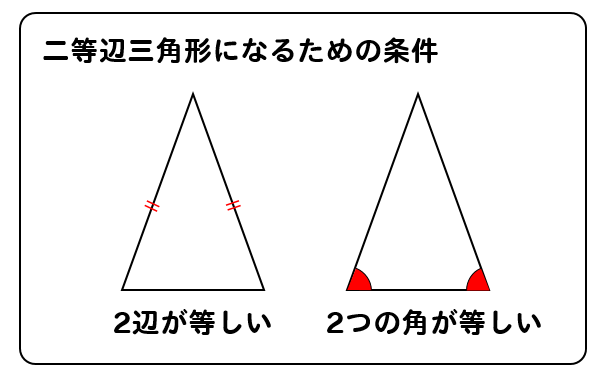
今回は中2数学で学ぶ、三角形の合同条件について勉強したいと思います。 三角形の合同条件 3つの辺がそれぞれ等しい 2辺とその間の角がそれぞれ等しい 1辺とその両端の角がそれぞれ等しい 三角形の合同条件を使った証明問題 問題① 〈解答〉 問題② 〈解答〉 問題③ 〈解答〉 スポンサー 合同条件1「3つの辺の長さがそれぞれ等しい」 「3つの辺の長さ」 がすべて等しいっていう条件は合同条件だ。 この条件を満たす三角形たちは合同である、ってことが言えるわけね。 たとえば、次の2つの ABCと DEFを想像してみて。 AB = 6 cm BC = 8 cm AC = 7 cm と、 DE= 6 cm合同式において,足し算,引き算,かけ算は普通の等式と同様に行ってOKですが,割り算は a a a と n n n が互いに素という条件がつきます(超重要)。
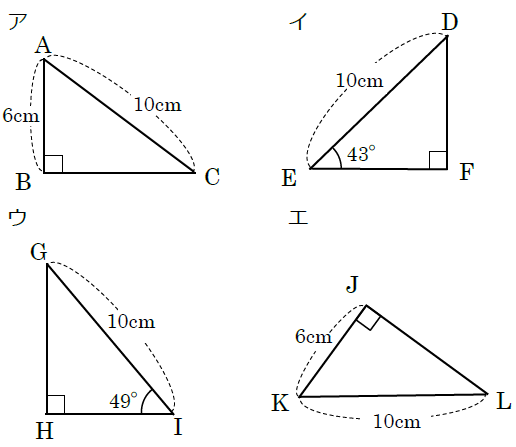
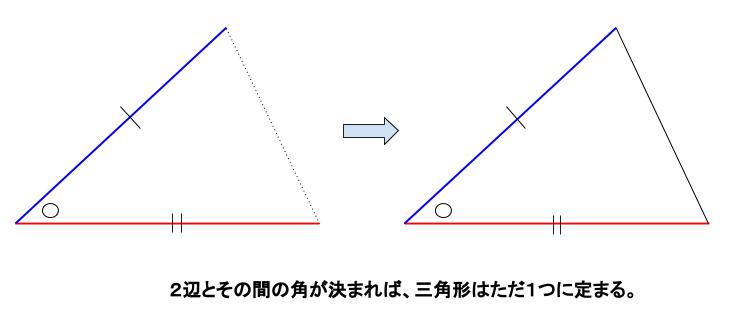
直角三角形の合同条件 以下の 2 2 つを利用します。 1 斜辺と 1 1 つの鋭角がそれぞれ等しい。 この 2 2 つは暗記してください。 三角形の合同条件 3 3 つを暗記しましたね? 同じことです、覚えないと話になりません。平行と合同 要点 平行線の錯角と同位角 内角の和、外角の和 合同条件 合同の証明三角形の合同条件 3組の辺がそれぞれ等しい 2組の辺とその間の角がそれぞれ等しい 1組の辺とその両端の角がそれぞれ等しい これらは重要なので3つともきちんと覚えましょう。 特に 「それぞれ」 という語句を忘れがちなので要注意。 どれも 「〇〇が



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




上数学合同条件 ニスヌーピー壁紙
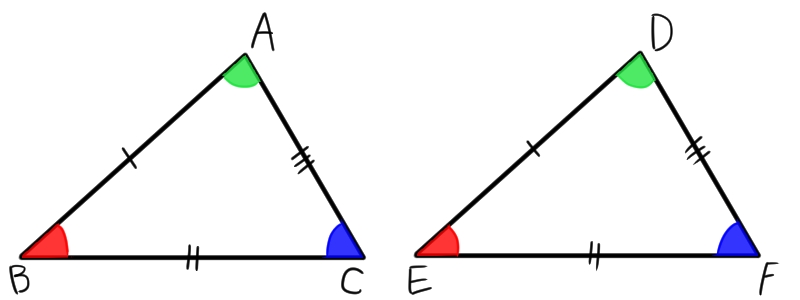
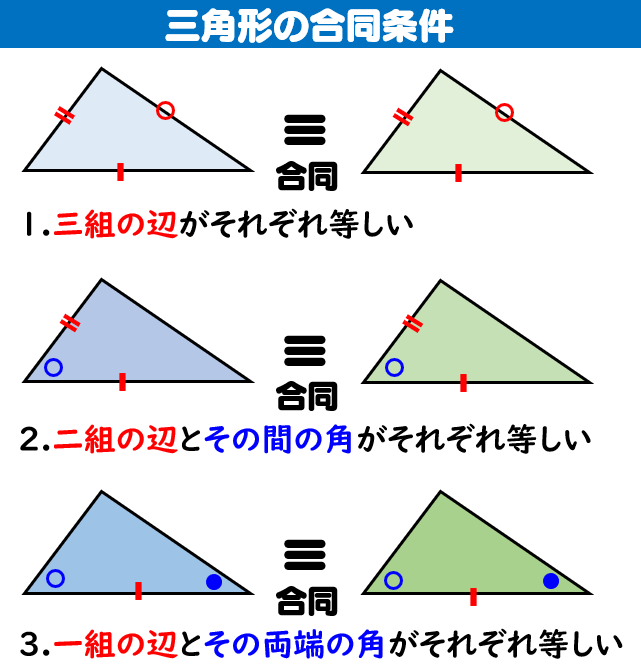
ここで三角形の合同条件を思い出して! 忘れた人はココ:三角形の合同条件 すると、 2組の辺とその間の角がそれぞれ等しい ので、 ade≡ acbとなる。 合同な図形では、対応する辺の長さが等しいので bc=edである。 ・・・(ここまでが答え)数学科学習指導案 1 単元名 図形の調べ方 2 本時の学習 三角形の合同(2/3) 3 本時の目標 ・ 三角形の合同条件を見いだすことができる。証明とは? 証明はハンバーガーだ1(1行目の書き方のコツ) 証明はハンバーガーだ2(中身の書き方のコツ) 証明はハンバーガーだ3(結論の書き方のコツ) 三角形の合同を証明する問題



三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト




数学 中2 56 三角形の合同 基本編 Youtube
証明に使う"合同条件"性質"まとめました。 良かったら、最後まで見てください! 学年 中学2年生, 教科書 未来へひろがる数学2 啓林館, 単元 証明, キーワード 数学証明,合同な図形と証明,合同关系是一个 等价关系 ,也就是说满足: 1、 反身性 :任意矩阵都与其自身合同; 2、 对称性 : A 合同于 B ,则可以推出 B 合同于 A; 3、 传递性 : A 合同于 B , B 合同于 C ,则可以推出 A 合同于 C; 4、合同矩阵的 秩 相同。 矩阵合同的主要判别法: 设A,B均为复数域上的n阶对称矩阵,则A与B在 复数域上 合同 等价于A与B的秩相同 设A,B均为实数域上的 n阶对称矩阵合同法 「合同」で始まるページの一覧 タイトルに「合同」を含むページの一覧 このページは 曖昧さ回避のためのページ です。 一つの語句が複数の意味・職能を有する場合の水先案内のために、異なる用法を一覧にしてあります。 お探しの用語に一番




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




直角三角形の合同条件とその証明 数学fun
合同条件と相似条件、三平方の定理や円周角の定理は楽勝だ! 数学で証明がきらい! という人って多いと思います。 僕はその元凶は中学生で習う三角形の合同と相似の証明問題が原因だと思うのです。 なぜですか? 図形の証明問題って基本的に計算が三角形の合同条件 三角形が合同であるためには、次の3つの条件のうち1つでも満たせばOKです。 3つの辺の長さがそれぞれ等しい この図形の場合 ・ab=de ・bc=ef ・ca=fd 2つの辺の長さと、その間の角の大きさがそれぞれ等しい直角三角形の合同条件とその証明|数学fu ・ 合同な図形を記号「≡」を使って表すことができる。・ 三角形の合同条件を利用して,図形のいろいろな性質を証明することができる。・ 仮定,結論を区別し,それを式などで表すことができる。




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ



中学2年生の数学 証明 三角形の合同条件と証明の書き方 塾講師が数学をやりmath
数学 合同 条件 従って、 1つの辺が等しく、その両端の角が等しい場合、合同であると言えます。 まとめ 三角形の合同条件は 3つの辺が等し 数学 中学数学 中学2年生 三角形の合同条件 一方の図形を移動させて他方の図形と完全に重なる時 、この2つの図形の関係を 合同 と言います。 合同であるとき、記号「 ≡ 」を使います。 三角形は毎回重ねる事をしなくても、共通点があれば合同であることが分かります。 この時の共通点が合同条件です。証明とは? 証明はハンバーガーだ1(1行目の書き方のコツ) 証明はハンバーガーだ2(中身の書き方のコツ) 証明はハンバーガーだ3(結論の書き方のコツ)




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学



中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su



中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




三角形の合同条件のなぜ 中2数学 Youtube




17考研数学 矩阵合同与相似的典型题型分析 文都考研网



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




國二junior High数学的数学図形角度まとめ 筆記 Clear



三角形の合同条件と証明問題の解き方 数学fun



中2数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
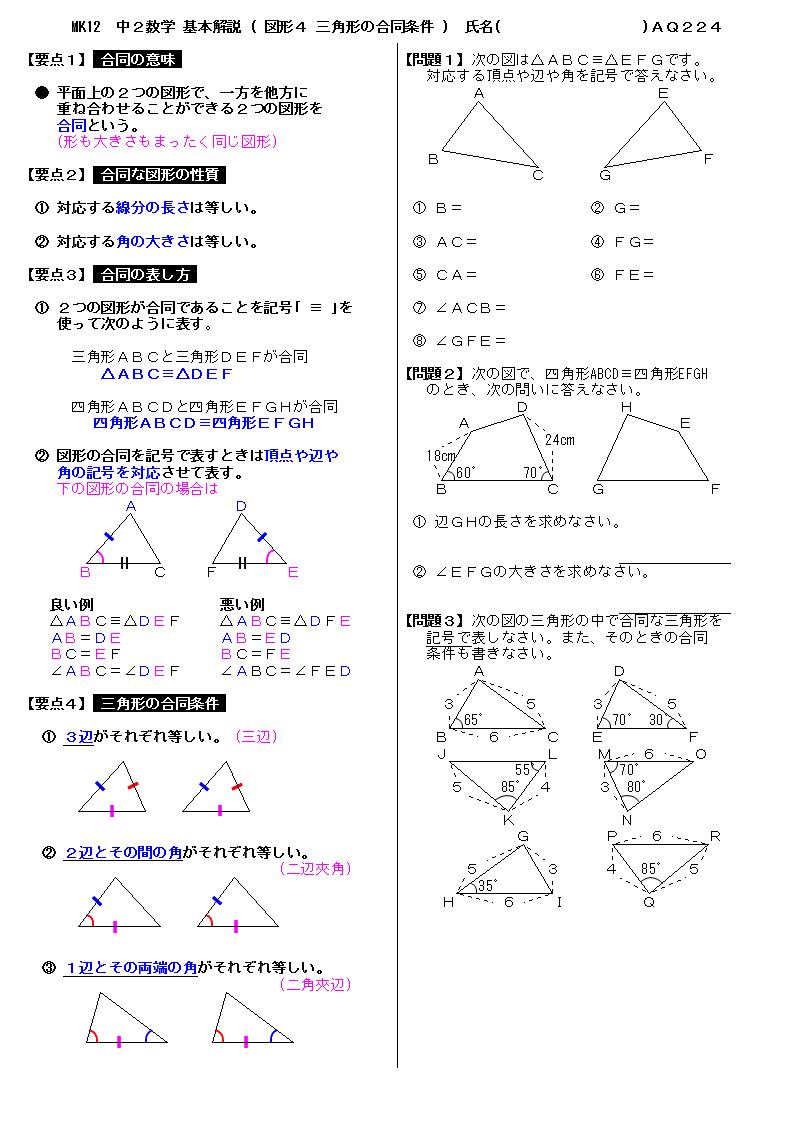



無料 中2数学 基本解説 問題プリント 224 図形4 三角形の合同条件




17考研数学 二 中如何判定矩阵合同关系 文都考研网




高一数学必修2知识点总结 Doc下载 Word模板 爱问共享资料




中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材




5分でわかる 三角形の3つの合同条件 Qikeru 学びを楽しくわかりやすく
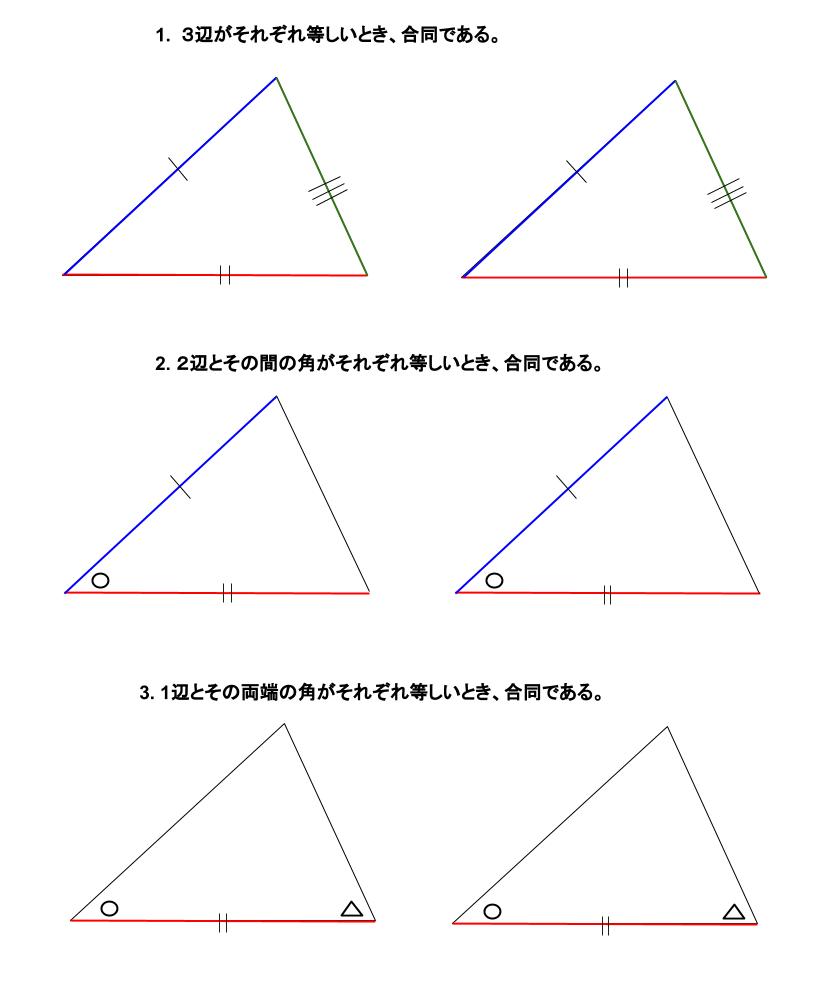



中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




中2数学 合同条件と定義 定理 性質の確認 赤城 ᐡᐤᐡ




中2 数学 合同4 合同条件 1辺と両端角 10分 Youtube
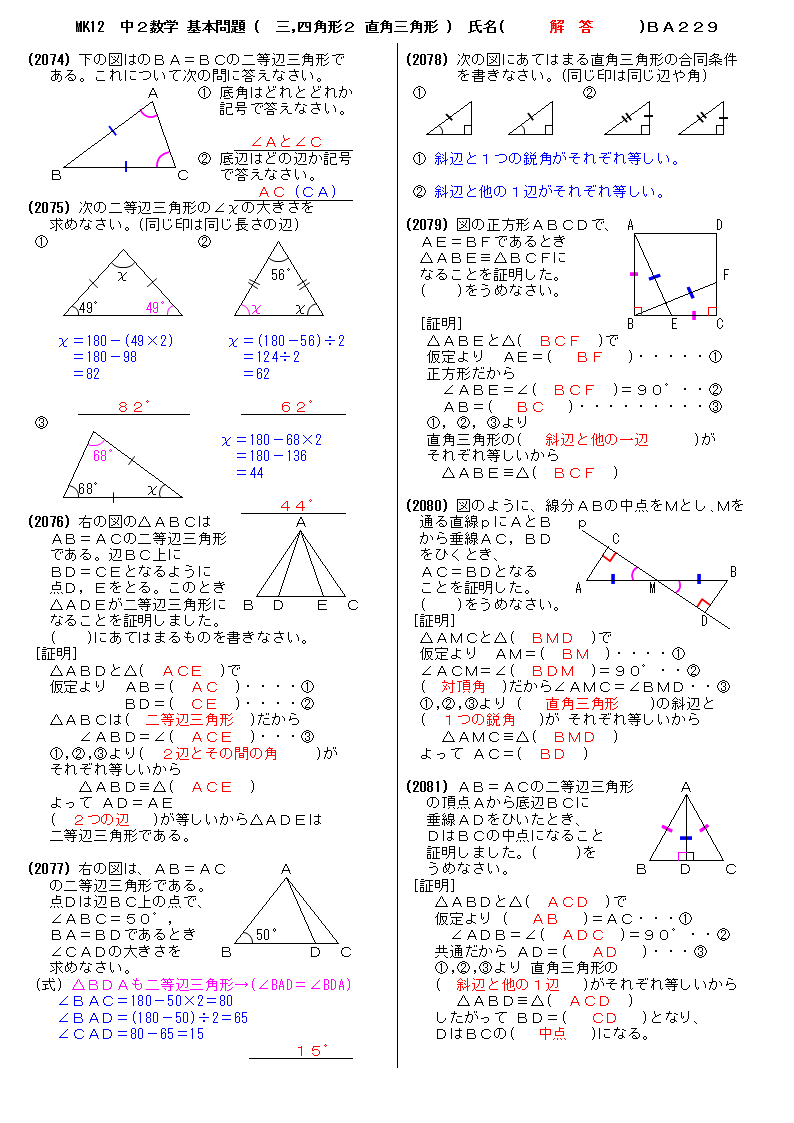



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形
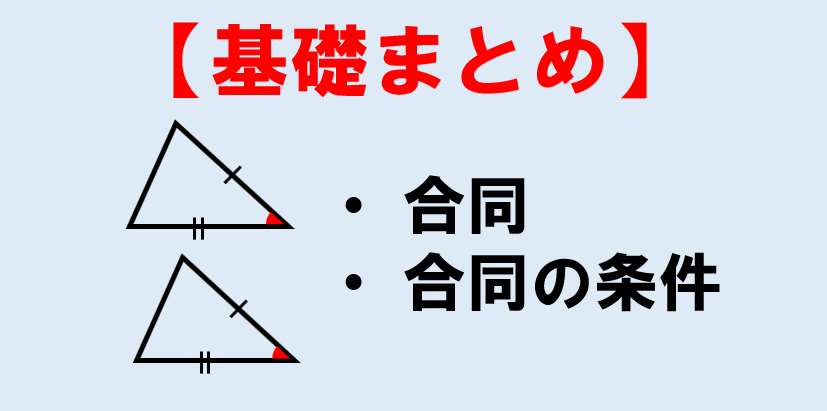



中2数学 合同 三角形の合同条件まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
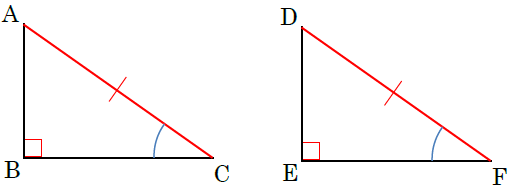



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ




三角形と四角形 三角形の合同の証明のしかた 中学数学 定期テスト対策サイト



上数学合同条件 ニスヌーピー壁紙
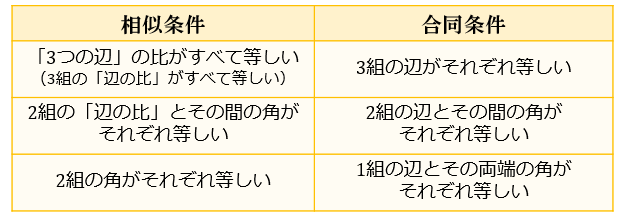



三角形の合同条件 相似条件と合同条件の違いとは アタリマエ



中学で習う 数学 合同条件全部教えてください 三角形の合同条件 3辺の Yahoo 知恵袋



矩阵的合同相似等价为什么这么定义呢 哔哩哔哩 Bilibili




三角形の合同条件 中学数学 By じょばんに マナペディア




数学 中2 58 三角形の合同 合同探し編 Youtube
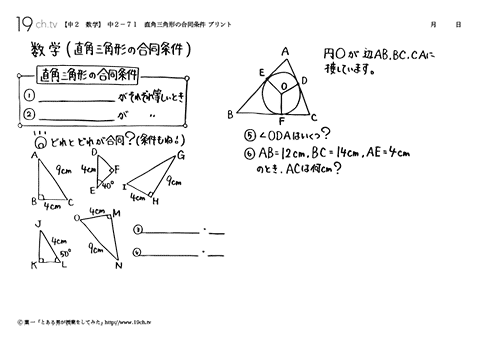



中学2年の数学 動画 直角三角形の合同条件の問題 19ch
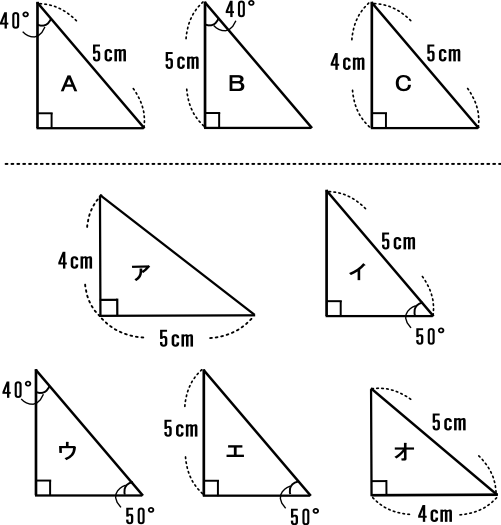



中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同
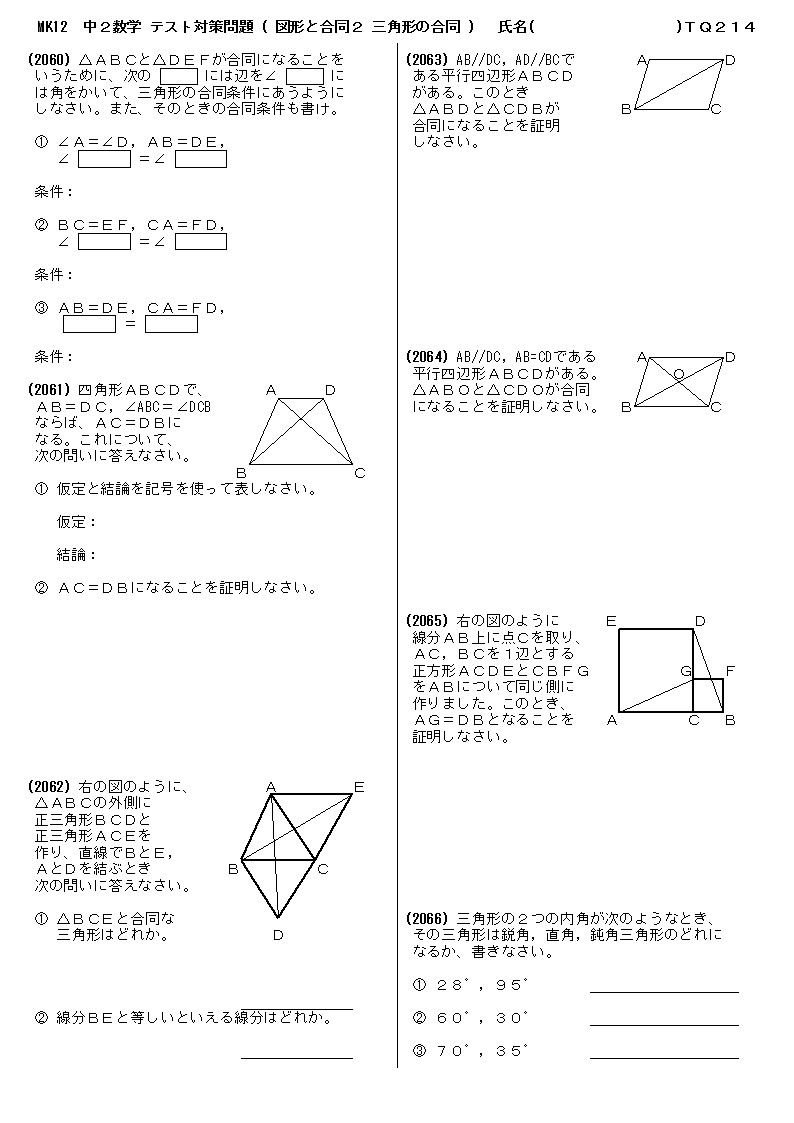



無料 中2数学 テスト対策 問題プリント 214 図形と合同2 三角形の合同




中2数学 三角形の合同条件3 1辺とその両端角 映像授業のtry It トライイット




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾




最も人気のある 三角形合同証明 ニスヌーピー壁紙



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典
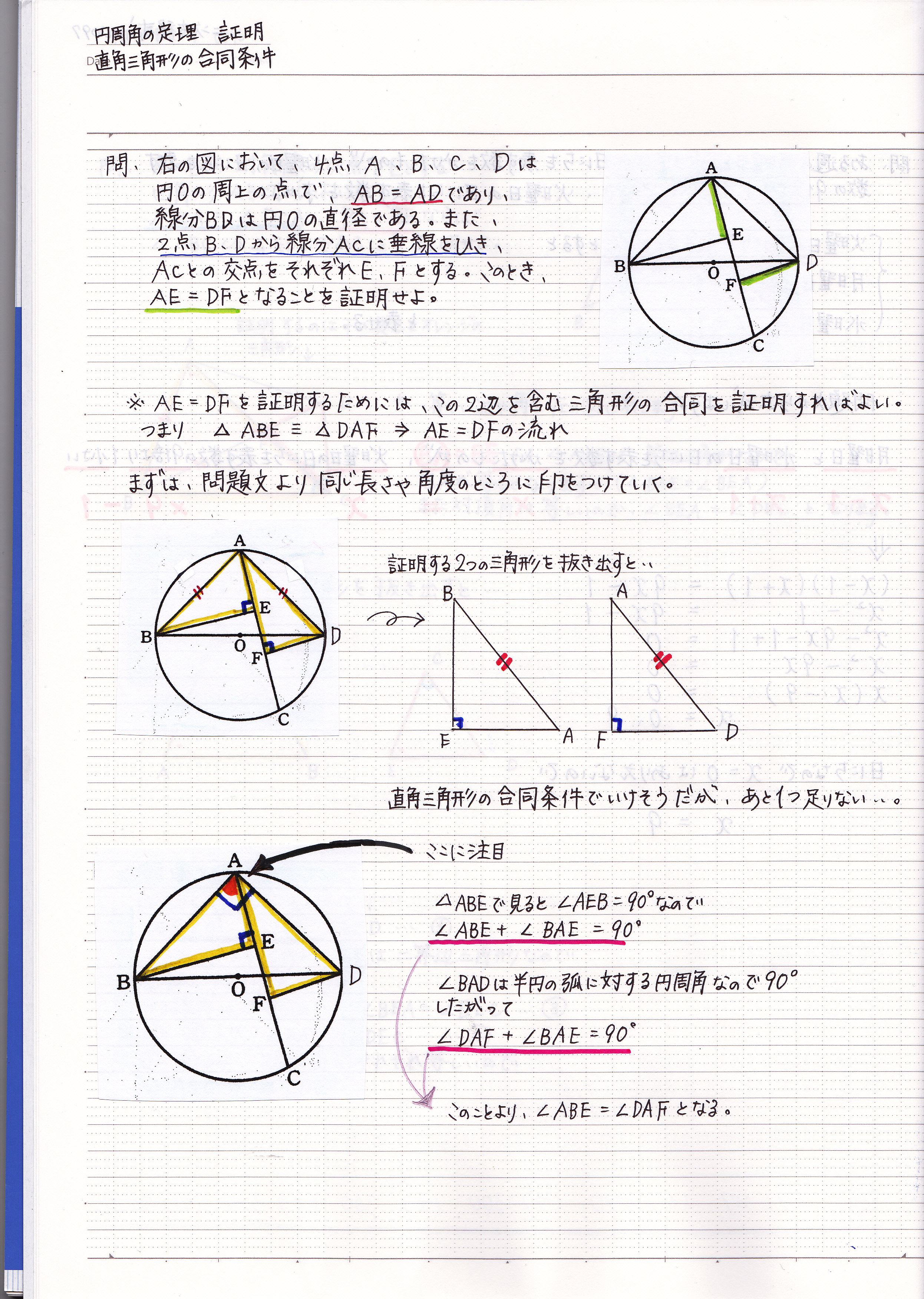



直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方
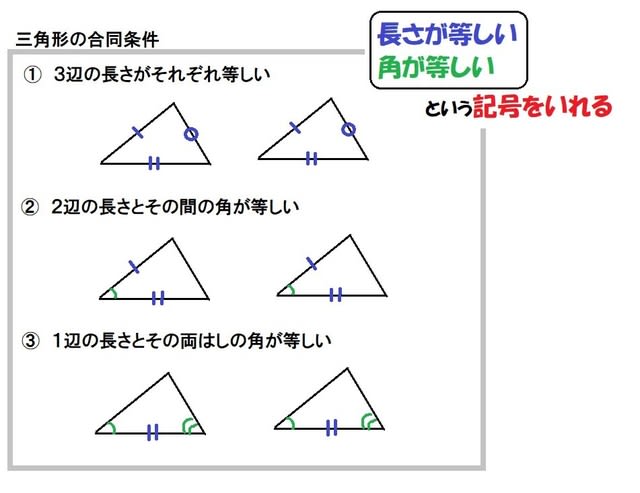



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support




中学生 三角形の合同条件のノート一覧 Clear




中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく
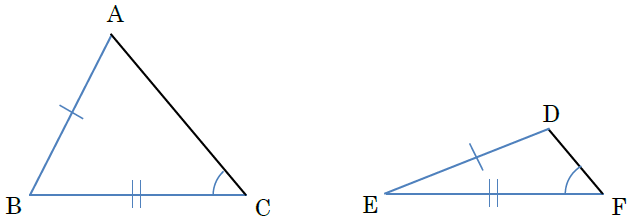



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
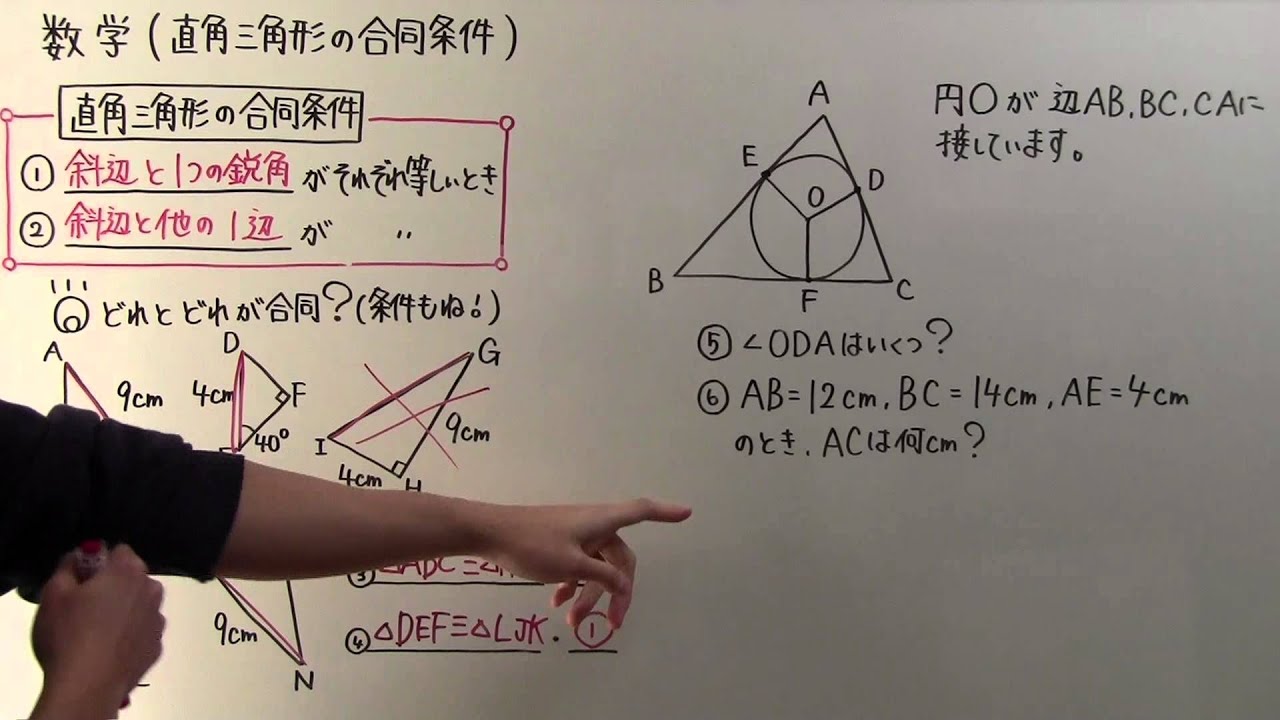



数学 中2 71 直角三角形の合同条件 Youtube




直角三角形の合同条件とその証明 数学fun
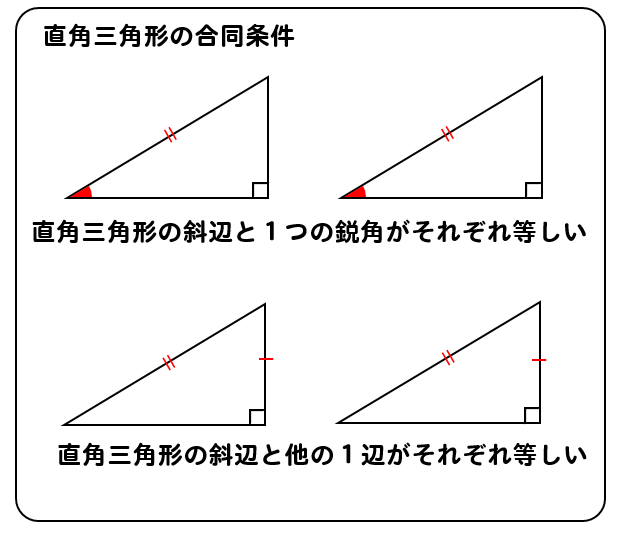



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




三角形の合同条件と証明問題の解き方 数学fun




三角形の合同条件 証明のときに絶対にしておかないといけない問題 中学や高校の数学の計算問題




直角三角形の合同条件 算数 数学が好きになりmath



新高一 数学第二课 集合知识点总结及练习题 综合




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
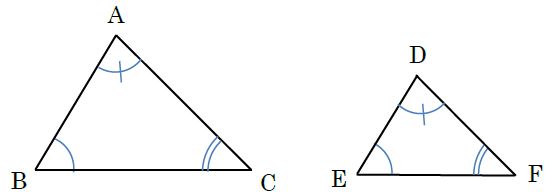



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




中2 中2 数学 主要合同条件 定理 定義 中学生 数学のノート Clear




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張




直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
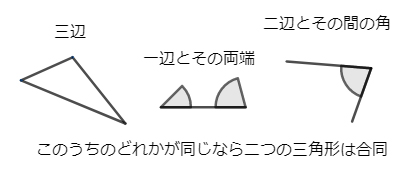



数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ
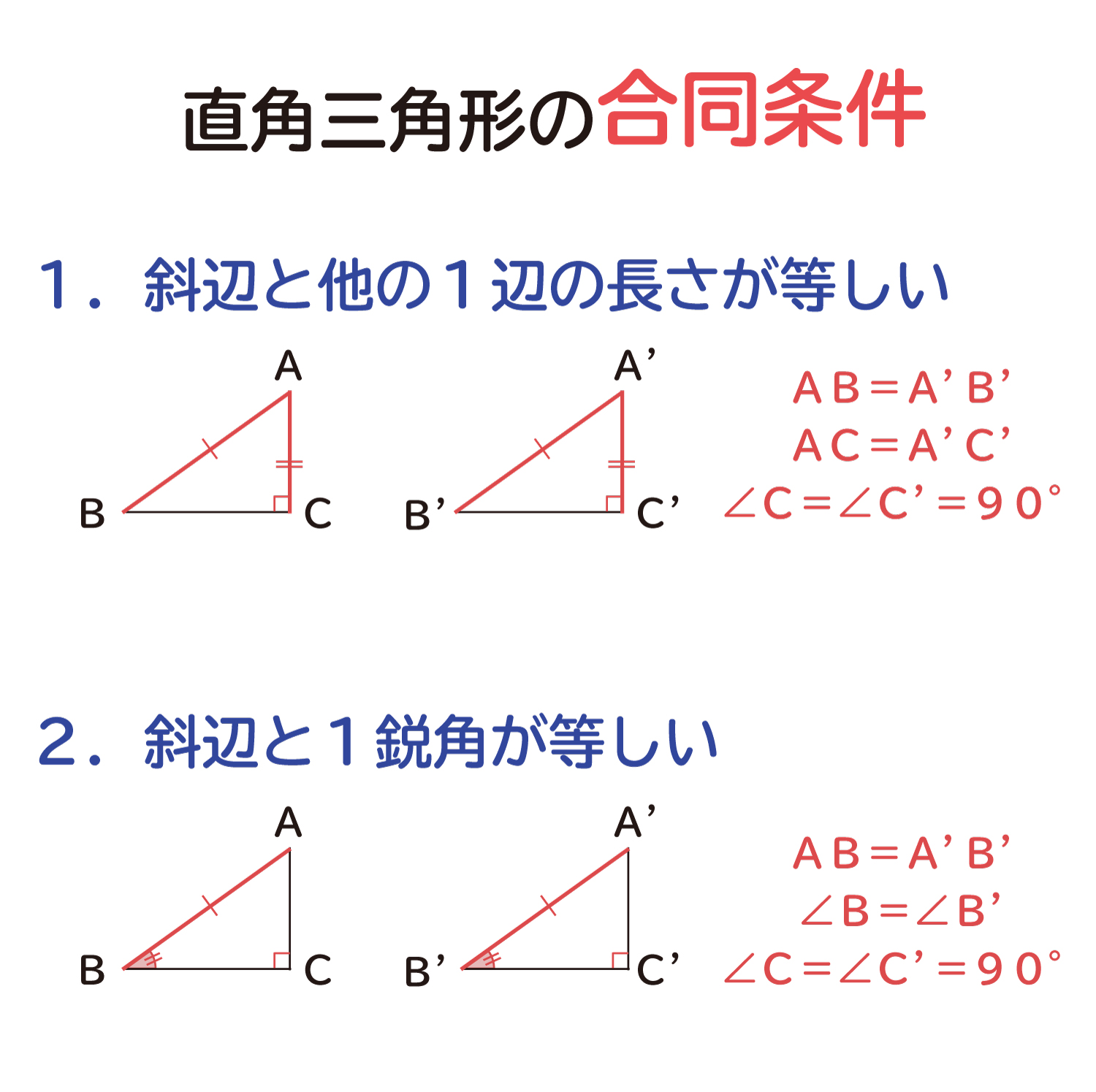



直角三角形の合同条件の説明 おかわりドリル




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




三角形の合同条件 相似条件と合同条件の違いとは アタリマエ



数学の合同の証明について模擬試験で 直角三角形の合同条件を使う問題で 間違えて Yahoo 知恵袋




中学生 三角形の合同条件のノート一覧 Clear




中2数学 三角形の合同条件2 2辺とその間の角 例題編 映像授業のtry It トライイット
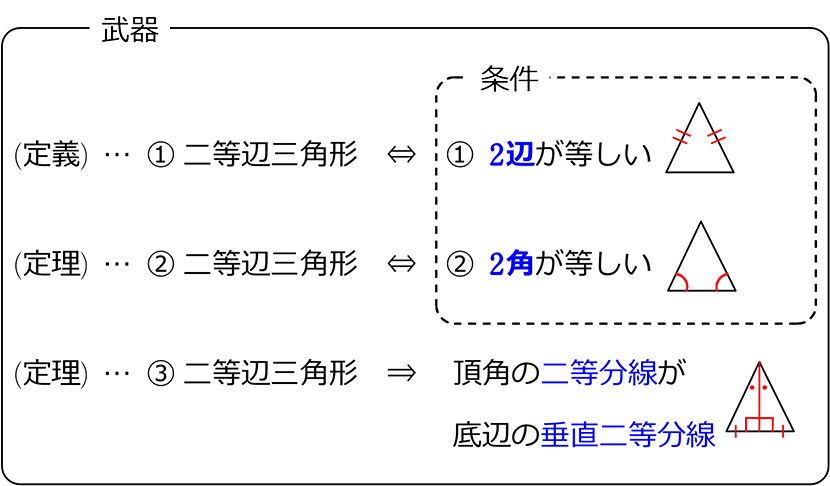



中学数学 図形の合同 図形の性質




直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




2 の直角三角形の合同条件は何ですか 理由も付けて教えて頂けると助かります Clear



水木艾迪考研数学解题36计之28 等价相似与合同下载 在线阅读 爱问共享资料




三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学
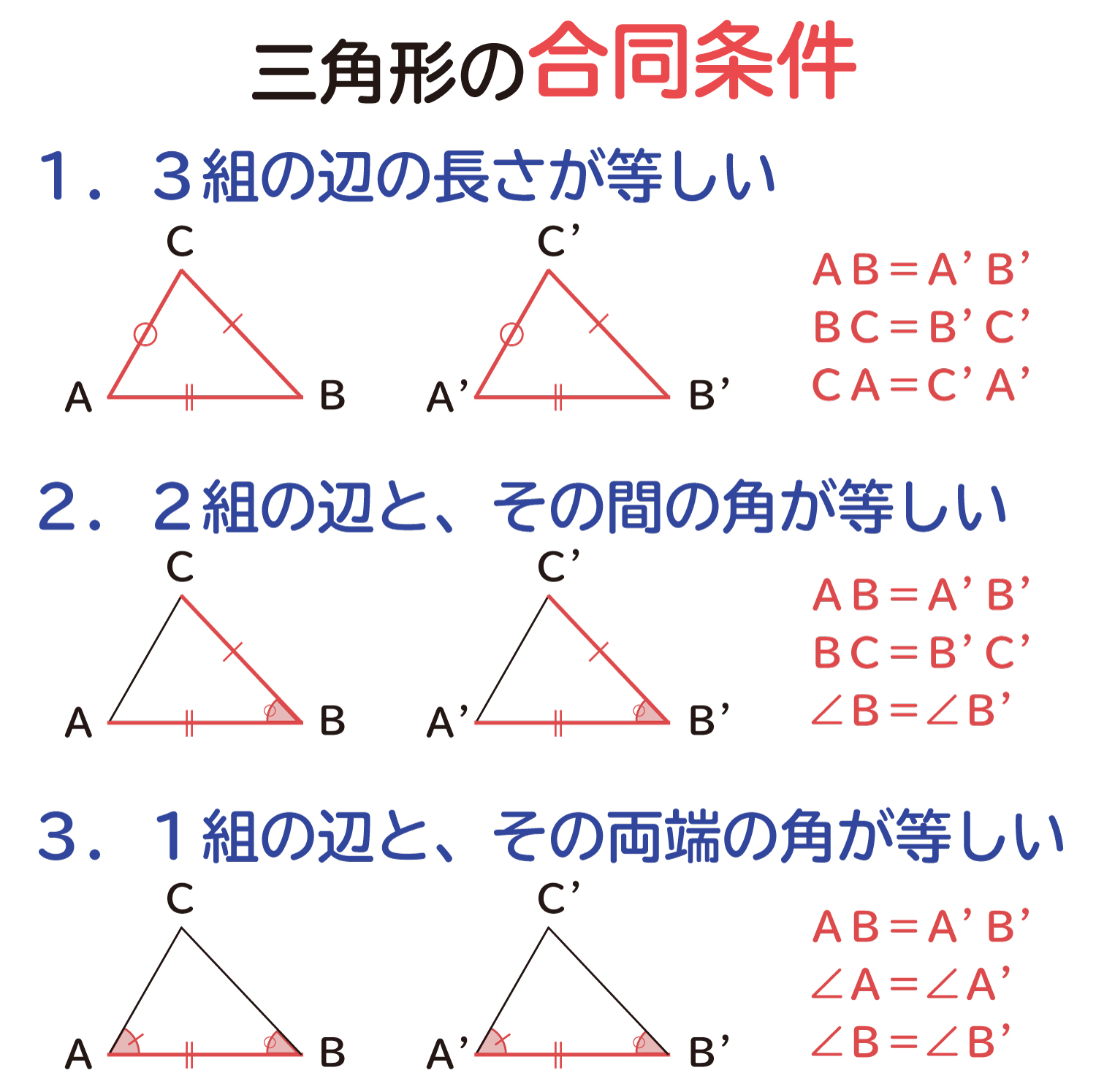



三角形の合同条件の説明 おかわりドリル




三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方
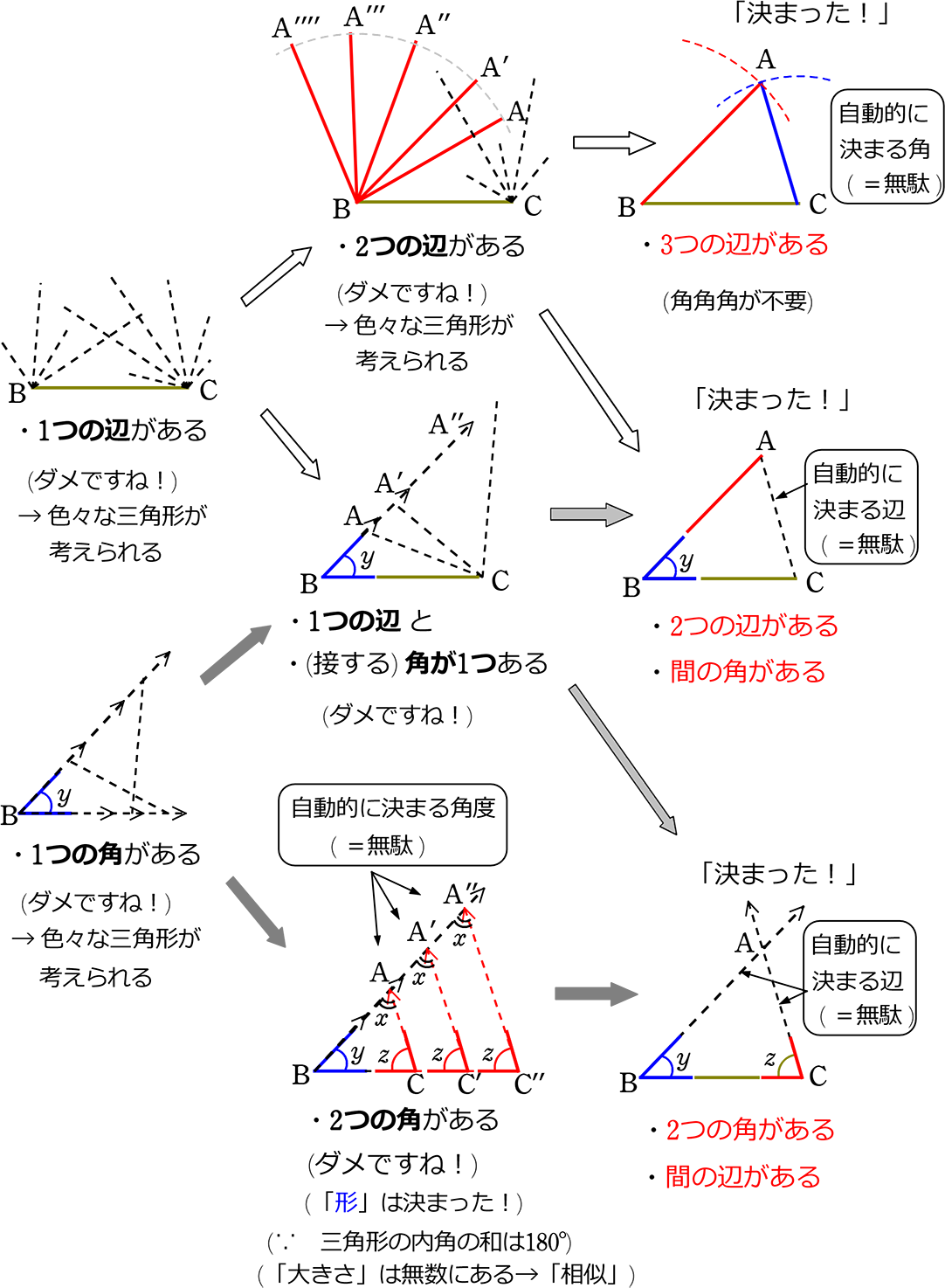



中学数学 図形の合同 図形の性質




中学数学より3 三角形の合同条件 身勝手な主張




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ




17考研数学 相似矩阵与合同矩阵的异同分析 文都考研网
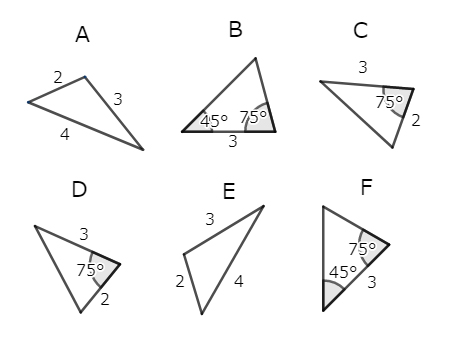



数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ




3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ




合同制 仲恺中学和潼湖中学再招2名控股初中数学老师 考试 笔试 应届毕业生 教师资格证 网易订阅




中2数学 三角形の合同を証明する問題 例題編 映像授業のtry It トライイット




菲迪克 Fidic 文献译丛 全4册 施工合同条件 简明合同格式 生产设备和设计 施工合同条件 设计采购施工epc交钥匙工程合同条件 虎窝淘




21年新书设计采购施工epc 交钥匙工程合同条件 原书17年版 菲迪克 Fidic 文献译丛书国际咨询工程师联合会机械工业出版社
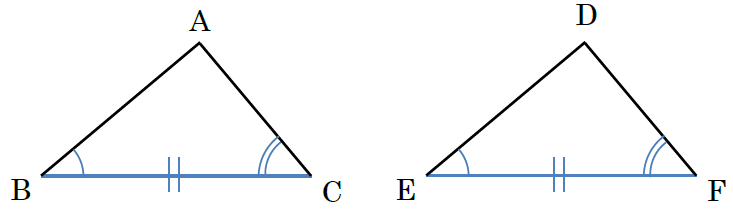



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
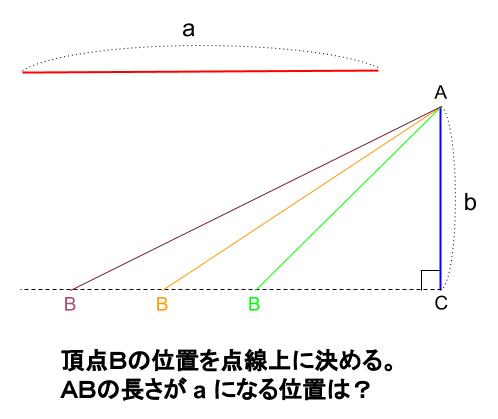



中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




中2数学 三角形の合同条件2 2辺とその間の角 練習編 映像授業のtry It トライイット
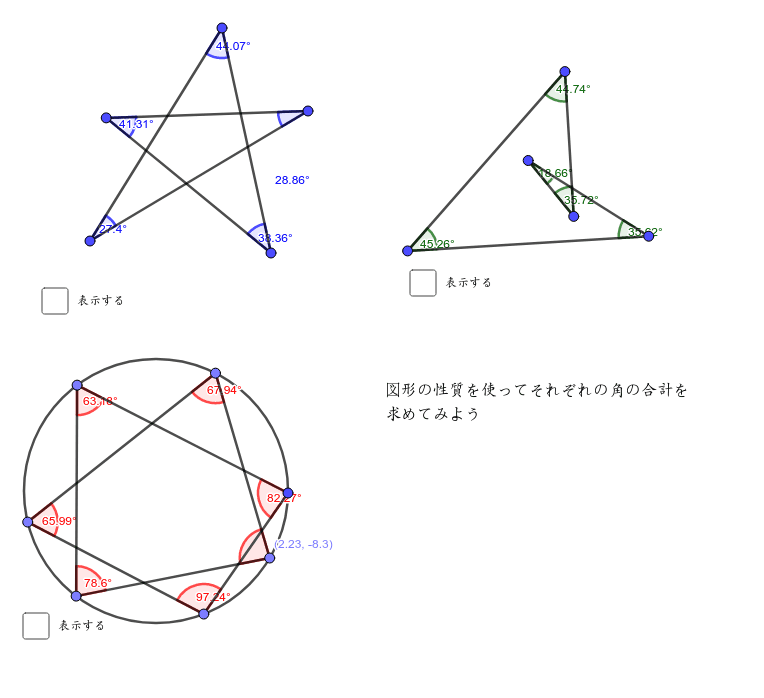



中2 数学 三角形の合同条件 角の和を求めてみよう Geogebra



考卷曝光 便利蜂若以 数学考试不及格 裁员涉嫌违法 正义网




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
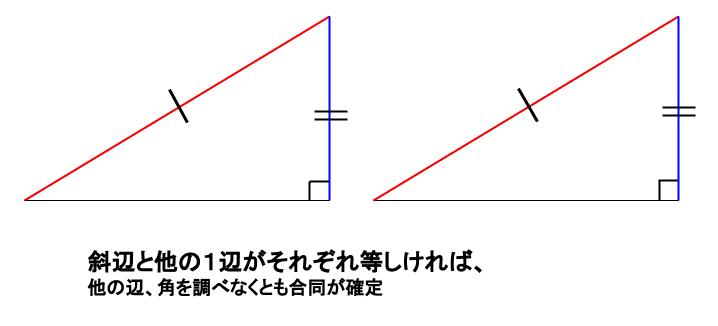



中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




三角形の合同条件 Youtube



上数学合同条件 ニスヌーピー壁紙



上数学合同条件 ニスヌーピー壁紙



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
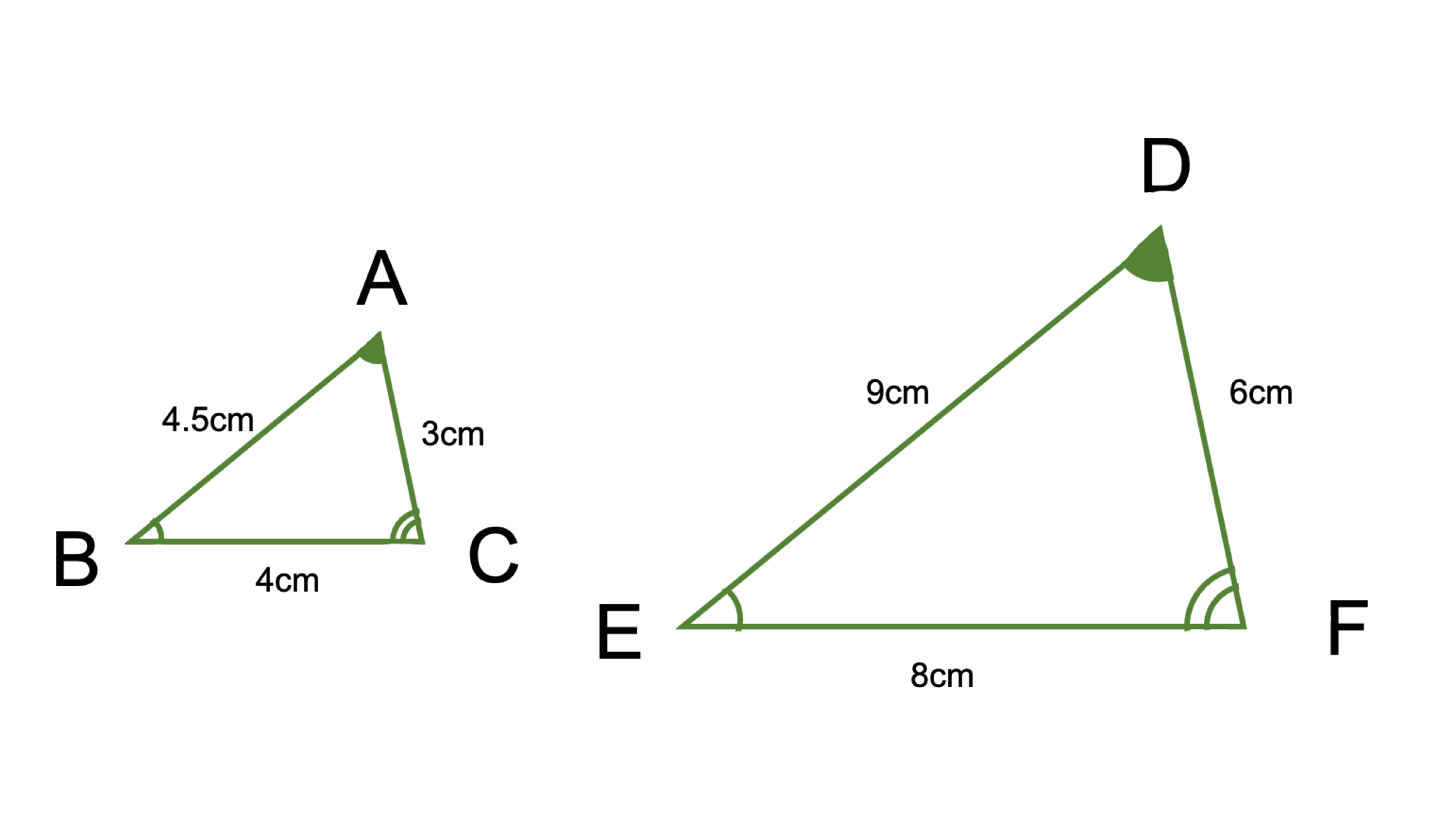



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



招聘 吉利中学招聘数学 政治 历史合同聘用制教师 禅城区



0 件のコメント:
コメントを投稿