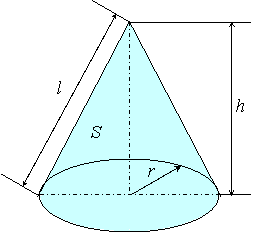
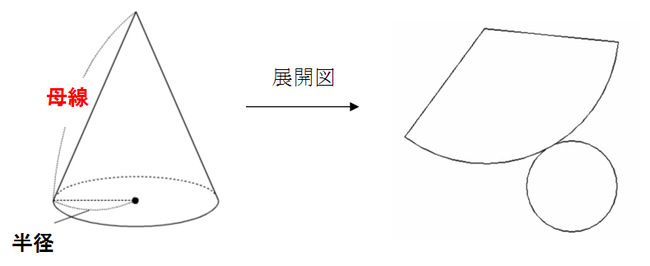
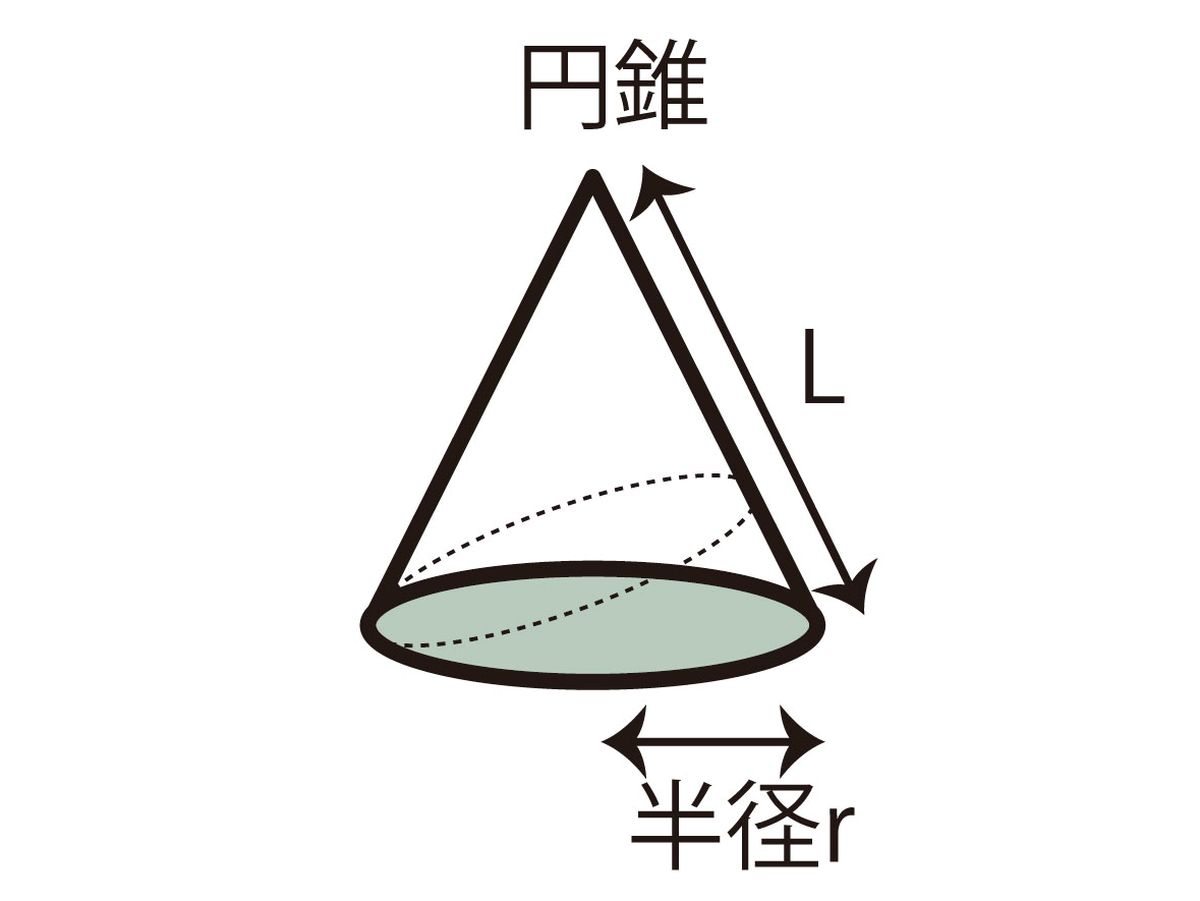
円錐台(えんすいだい、英 circular truncated cone )は、円を底面とした錐台である。 つまり、円錐を底面に平行な平面で切り、小円錐の部分を除いた立体図形である。 プリンの形は一般的には円錐台である。受験数学、特に日本の中学入試でよく出題される図形である。円錐の体積 円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより側面積(扇形の面積)は,π×× nnn = 16 π 底面積と側面積(扇形の面積)を加えると,表面積は π (2) 底面は半径 3 の円だから,底面積は π×32= 9 π 展開図において扇形の中心角を x° とおくと,扇形の弧の長さが底面の円周の長さと等しくなる

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
円錐 の 公式 は
円錐 の 公式 は-3 円すい展開図・表面積の公式 の求め方 31 一つの式で書く;鏡板の計算 入力欄に数値を入力して「計算」ボタンをクリックしてください。 D:内径 / R:中央部の内半径 / r:すみの丸みの内半径 / t:厚さ / ℓ:フランジ部長さ / H:高さ / TL:タンジェントライン *鏡板中心軸における内頂点からの距離 代表



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
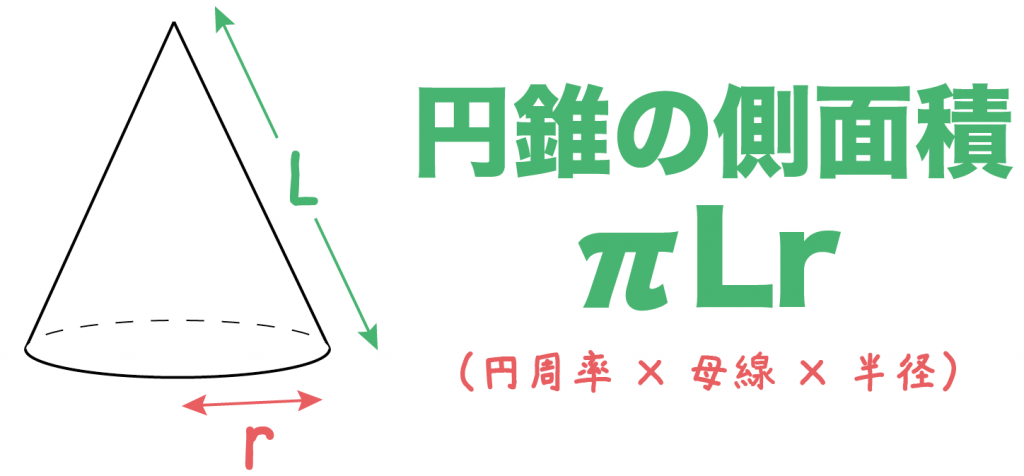
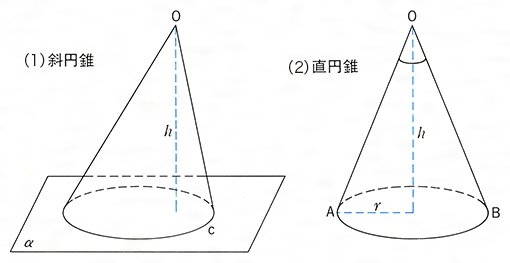
円錐の側面積 の公式• s:へー。 また、円 O をこの斜円錐の 底面、点 p をこの斜円錐の 頂点という。 なお、斜円錐の頂点 p から平面 P に下ろした垂線の足が円 O の中心に一致するならば、この斜円錐は直円錐円錐定義は後述をある平面で切断したときに切断面に現れる曲線を総称して円錐曲線という。 円錐曲線には楕円,円,放物線,双曲線がある。 (1) メナイクモス 円錐曲線はメナイクモス( M enaiqmoc (Menaichmos ,Menaechmus) BC4 世紀) によって発見さ れたといわれている。 こんにちは。相城です。円錐関連の公式の導出を書いておきます。単純に公式を暗記するのではなく, 覚えられる方は理屈も確認しておきましょう。 円錐の展開図において, 側面のおうぎ形の半径(円錐の母線)を, 側面のおうぎ形の弧
2 公式を使わない解答 21 おうぎ形の弧の長さを求める;おうぎ形の面積 半径の長さr、中心角α°のおうぎ形の面積Sは、 \begin {eqnarray*} && { \Large S=\pi r^2 \times \frac {α} {360} } \ \end {eqnarray*} この式で、「π×rの2乗」の部分はご存知、半径rの円の面積を表しますよね。特に円錐では,底面の半径をrとすると だから になります。 ⇒高校数学の積分を使えば証明できるが,小中学校でもこの公式は登場するので,結果を先取りして「柱の体積÷3」と覚えてしまう方が早い
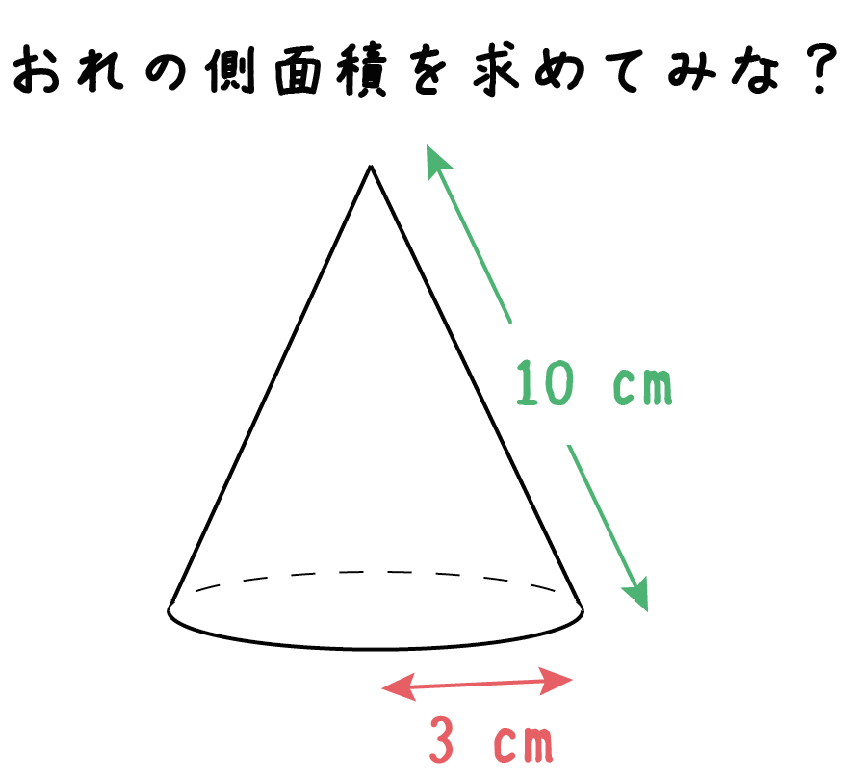
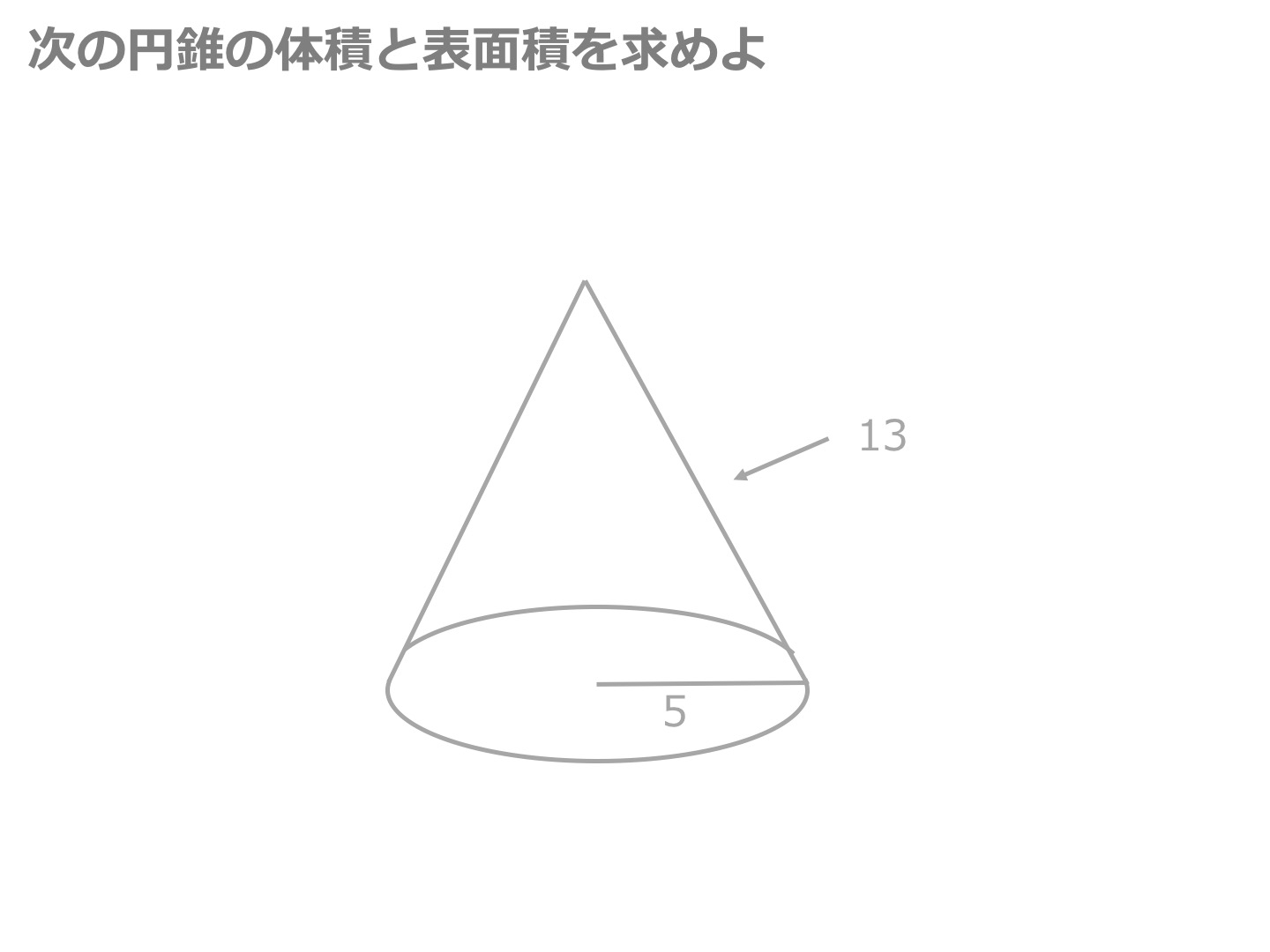
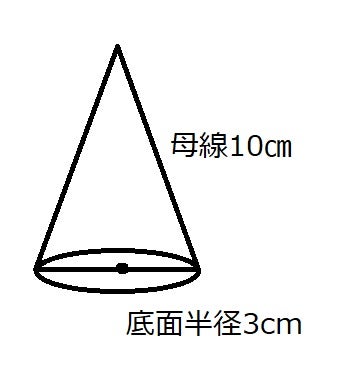
まずは公式にしたがって円錐の底面積を求めましょう。 底面積 $$\pi \times 3^2=9\pi(cm^2)$$ 次は母線と半径をかけて、側面積を求めます。 側面積 $$8\times 3\times \pi=24\pi(cm^2)$$ 底面積と側面積がそれぞれ求まれば、あとは合計すれば終わり。 表面積長さ l m の糸の一端を固定し、他端に質量 m kg のおもりを吊るして、このおもりを水平面内で等速円運動させたときの円錐振り子 * 糸の運動面が円錐(えんすい)形になるので「円錐振り子」です。 おもりを鉛直面内で振らせれば 単振り子 です。 閉じる の運動について考えてみます。 鉛直線と糸とのなす角を θ rad 、糸の張力を S N 、角速度を ω rad/s立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm



1




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
円錐の中心角の求め方は、 扇部分の半径・弧の長さを求める (扇の中心角を求める問題になる) 中心角を求める はかせちゃん 今日もお疲れ様でした! 抹茶ラテ飲んでゆっくりしましょ~ 関連記事はこちら 中学数学円錐の表面積の求め方と公式図底面積 は,半径5cmの円の面積なので, π × 5 2 = 2 5 π ( c m 2) \pi×5^2=25\pi (cm^2) π × 52 = 25π(cm2) 高さ は9cmなので, (底面積)× (高さ)= (体積) より, 2 5 π × 9 = 2 2 5 π ( c m 3) ‾ 25\pi×9=\underline {225\pi (cm^3)} 25π × 9 = 225π(cm3)円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




公式を図解 すい体の体積 円すいの表面積の求め方
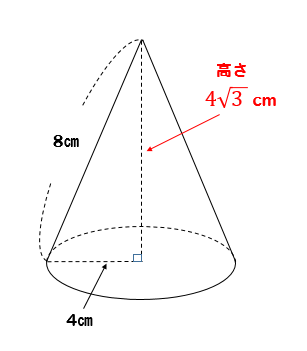
円錐の高さ=円錐の体積÷底面積×3 で求めることが出来ます。 ここで、底面積=10×10×314=314 よって求める円錐の高さ=1570÷314×3=15(cm) 答え 15cmπ b 2 × b h a − b × 1 3 = π b 3 h 3 ( a − b) です。 一方、大きな円錐の高さは、 x h = b h a − b ( a − b) h a − b = a h a − b となります。 したがって、大きな円錐の体積は、 π a 2 × a h a − b × 1 3 = π a 3 h 3 ( a − b) となります。 よって、円錐台の体積は「大きな円錐の体積」から「小さな円錐の体積」を引いたものなので、 1 公式を使った解答 11 円すいの表面積の公式;




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
円錐の体積を求める公式は、 V = 1/3 Sh = 1/3 πr^2 h で表されます。 このページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。円錐を平面で切断すると,楕円,円,放物線,二直線,双曲線となりますが, この式を良く見ると, の四次式ですが, の項がないので, の二次方程式の解の公式6、シンプソンの公式 (面積も体積も出せる万能公式) T:a=底面の面積 b=上面の面積 c=aとbの真中の面積 h=高さ とすると、 SorV=(a+b+4c)/6×h という公式がある。 この公式は、台の体積はおろか、三角形の面積まで求めることができる。 例えば、台形、半球を求めてみよう。 台形の面積=(a+b+4(a+b)/2)/6×h=(a+b)/2×h 半球の体積=(πr2+3



中学数学 円錐関連の公式の導出 数樂管理人のブログ




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
直円錐の体積 斜切円錐の体積 一部が欠けた直円錐の体積 円錐台の体積 楕円錐の体積 楕円錐台の体積 球の体積 一部が欠けた球の体積 弓形の回転体の体積 一部が欠けた弓形の回転体の体積 半球台の体積 円環体の体積 楕円体の体積 一部が欠けた楕円体の体積 スーちゃん 円すいの体積は円柱の3分の1ってならったよ森羅万象博士 三角すいや四角すいも3分の1になるね。なんでだろう。スーちゃん えっ 円錐の側面積の公式 まずは、公式だけ図でさっと確認するよ つぎに、円錐の特徴を確認して、そのあとに側面積を求めていくよ 円錐の特徴 円錐の特徴は主に次の二つだよ




空間図形14 円すい台の体積 Youtube




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
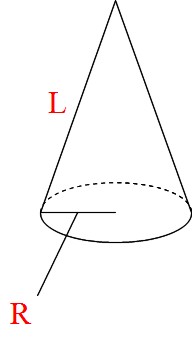
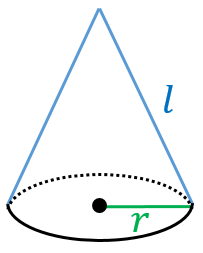
これは大事な公式ですからしっかりと覚えておきましょう。 円の面積の求め方は、 (円の面積) = (半径) × (半径) × (円周率π) ですね。 ここまでわかれば、準備完了です。 ・底面の円の面積は 3×3×π=9π㎡ ・高さは 8cm よって、求める円柱の円錐の表面積を求める公式 は、次の通りです。 S = πr(r R) = π ×(底面の半径)× {(底面の半径) (母線の長さ)} S = π r ( r R) = π × (底面の半径) × { (底面の半径) (母線の長さ) } 底面の半径 r、母線の長さ R の円錐 1行目の文字について、S は円錐の表面積、r は底面の円の半径、R は母線の長さを表します。 手っ取り早く円錐の体積を求めるには、この 赤い円 の円周の長さは 直 径 直 径 × 314 = 3 × 2 × 314 = 14 c m




円錐 Wikipedia




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学
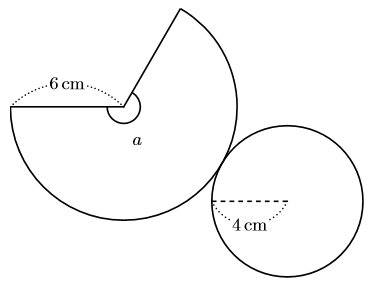
円錐の側面積と中心角を一瞬で求めてしまう裏ワザ公式です! まぁ、受験ではほとんどの人がこの裏ワザ公式を利用することになると思います。 だって、めっちゃくちゃ簡単だから。 そんな裏ワザ公式とは 母線と半径の長さを利用して円錐台の体積=底面積aの円錐の体積-底面積bの円錐の体積に当てはめると、 = となります。 この公式なら、aとbを同じにしても、bを0にしても矛盾は出ません。 シンプソンの公式 そうすると、先ほどの式は、 = となります。 これが、「シンプソンの公式」です。




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ



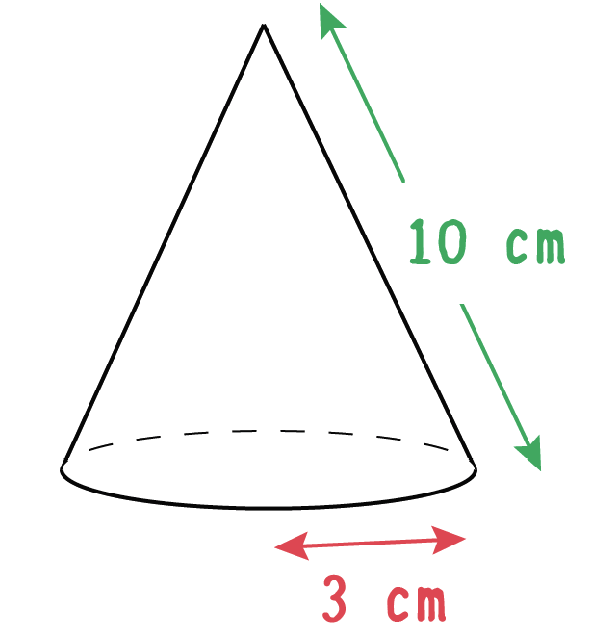
三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



数学の公式集 No 012 幾何図形 円錐の体積と表面積




円すいの展開図 中心角の公式を知って5秒で解こう



1




円錐の体積ってなんであの公式なの Webty Staff Blog



円錐の空間図形から表面積を求める基本公式と裏技 現役塾講師のわかりやすい中学数学の解き方




円錐の表面積を 公式を使って求める チーム エン




公式一覧 立体の体積 表面積の求め方 円柱 三角柱 円錐 三角錐 球



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



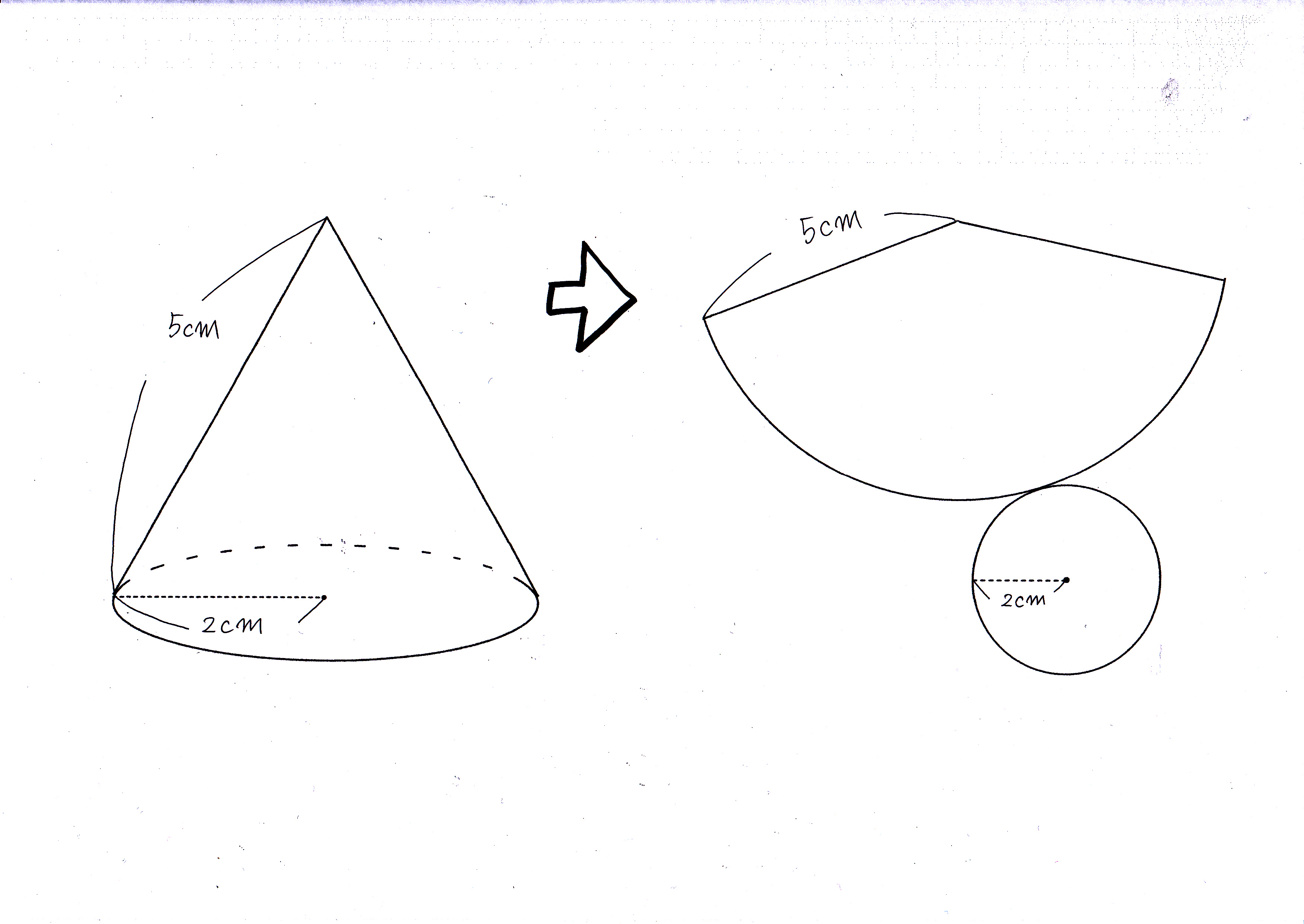
円錐の側面の展開図の扇形の中心角の公式が360 L Rになるのはな Yahoo 知恵袋




高校入試対策数学 円錐に関する対策問題 Pikuu




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




至急です 空間図形の問題がわかりません 解説お願いします Clear




円錐の体積の求め方 公式と計算例




円錐の体積ってなんであの公式なの Webty Staff Blog




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



3分でわかる 円錐の体積 表面積の求め方 合格サプリ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積 Youtube




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



1




Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su



1




どうして1 3なの 錐の体積の公式の求め方 まなべーと




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




円錐の表面積の求め方 公式と計算例




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo




直円錐の体積 高精度計算サイト



数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師




公式を図解 すい体の体積 円すいの表面積の求め方




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積 あんず学習塾のメモ 図表置き場




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




球の表面積と体積の公式 数学fun




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積 Youtube



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ



円錐とは コトバンク




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




公式を図解 すい体の体積 円すいの表面積の求め方



円錐の表面積の公式 オリジナル 学習塾サンクス ワン




円錐の表面積の求め方 公式と計算例




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題



数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo




中学数学の裏技 円錐の表面積を 10秒 で求める方法 Tara Blog



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



円錐の表面積の公式の求め方 中学数学



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学



Descubre Como Resolverlo En Qanda




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




現役塾講師直伝 円錐の表面積を求める 裏技 Kouの学び部屋



円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ




円錐の表面積の求め方 公式と計算例




円錐の体積を求める Youtube




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




積分を用いた円錐の体積公式の導出 頭の整理




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




ม 1 โน ตของ 中1数学 円錐の表面積のポイント ช น Junior Clear




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
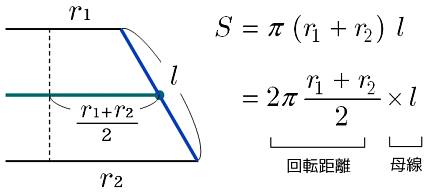



初等幾何 円錐台の側面積を求める 大人が学び直す数学




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の体積の求め方 公式 小学生 中学生の勉強




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学



円錐とは 体積 表面積の公式や求め方 受験辞典
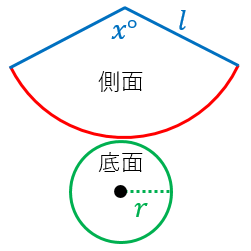



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学



しょうちゃん 公式ブログ 三角すい 四角すい 円すいの体積 Powered By Line




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




角錐 円錐の体積と表面積の公式 数学fun
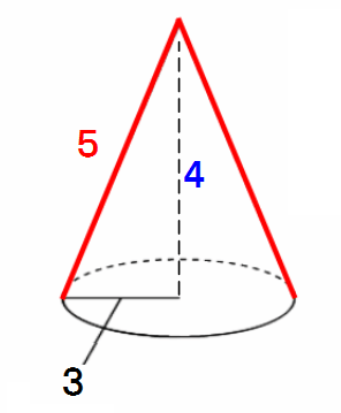



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




円錐の表面積の求め方 公式と計算例



0 件のコメント:
コメントを投稿