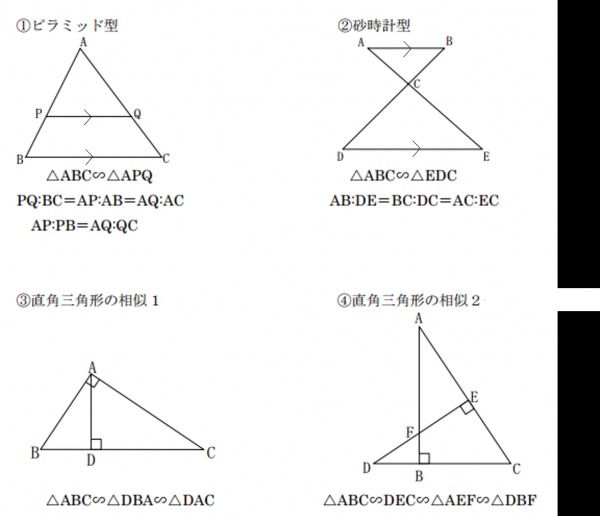
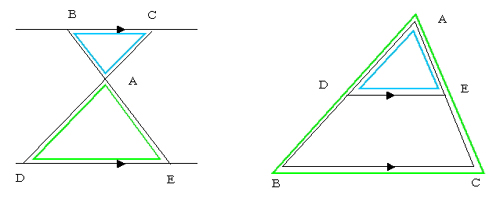
三角形 相似条件 三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分か Microsoft Powerpoint Lec07 Pdf Free Download 直角 三角形 の 相似 条件 比如当三角形为直角三角形时的反a字形。 应用举例 思路分析: 通常来讲,题目中遇到线段成某个比例的已知条件,往往会和三角形相似结合起来。因为三角形相似就能利用线段的比例。 三角形の相似条件は ① 3組の辺の日が等しい。 ② 2組の辺の比とその間の角が等しい。 ③ 2組の角が等しい。
1
直角三角形 相似条件
直角三角形 相似条件-動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaruまずは1つめ。「直角以外の角が等しい」 これは先程の三角形の相似条件② 三角形の合同ではなく直角三角形の合同条件で求めることはできませんか? 直角三角形を使わない理由が知りたいです 勉強Q&A ログイン 新規



相似三角形的判定 相似ppt 第3课时 第一ppt
《探索三角形相似的条件一》教学设计方案宜君县地区太安中学学校姓名屈莉莉课题名称 《探索三角形相似的条件一》 科目 数学 年级 八年级 教学时间 1课时40分钟 学习者分析 学生的知识技能基础学生以前学过平行线的条件有此知识作基础进一步学习三角形相似的条件相信学生不难理解和掌握本問2 下の図の三角形を、合同な三角形の組に分けなさい。また、そのとき使った合同条件をいいなさい。 3㎝ 3㎝ 3㎝ 3㎝ 5㎝ 5㎝ 5㎝ 5㎝ 5㎝ 5㎝ 70° ° ア イ ウ エ オ カ (4)任意相似直角三角形360旋转模型倍长法 条件:oabodc;oab=odc=90;be=ce; 结论:ae=de;aed=2abo 辅助线:延长de 至m,使me=de,将结论的两个条件转化为证明amdabo,此为难点, 将amdabc 继续转化为证明abmaod,使用两边成比例且夹角相等,此处难点在 证明
三角形相似条件、证明doc,三角形相似条件、证明 一、判断三角形相似(与全等的对比) 相似三角形定义:三角分别相等,三边成比例的两个三角形 全等(特殊的相似) 相似 asa 两角对应相等的两个三角形相似 aas sas 两边对应成比例,且夹角相等的两个三角形相似 sss 对应边成比例的两个三角形直角三角形相似的条件,用字母表示 作业帮 : 三边对应成比例、两边对应成比例且夹角相等、两角对应相等、平行于一边的直线截三角形另两边或延长线所得三角形与原三角形相似、定义、三边互相平行或三角形の相似条件は3組の辺の比がすべて等しい、2組の辺の比とその間の角がそれぞれ等しい、2組の角がそれぞれ等しい 相似条件とは?三角形の相似条件はなぜ3つなの?証明問題 直角三角形の相似 相似の証明でも取り扱った「直角三角形の相似」です。
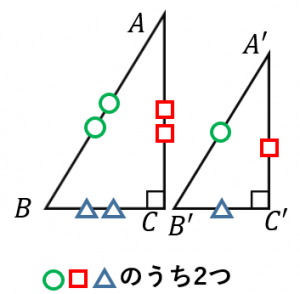
② 直角三角形の斜辺と他の 1 辺がそれぞれ等しい どちらの条件も「直角と斜辺は等しい」ので、違いは 1 カ所だけになります。 残り 1 カ所の等しい箇所が 「角」 なら、 (例) ∠ B = ∠ E → ① 直角三角形の斜辺と 1 つの鋭角がそれぞれ等しい相似形⑵ 直角三角形型相似② 2 ステップ1 正方形が入っている問題 1 図のように、直角三角形ABCの中に正方形がちょうど入っています。 ⑴ 三角形ABCの角Aの大きさを 、角Bの大きさを×とします。図 つぎの条件は、 2つの角が等しい条件 だ。 2つの角が等しいことを使った条件が、なんと偶然にも合同条件と相似条件に1つずつ存在しているんだ。 合同条件2 「1つの辺とその両端の角
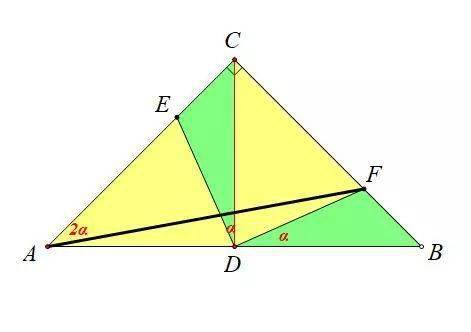



中考数学 等腰直角三角形 套路深 竟有这么多 基本图形 几何




超级精品 初中数学几何模型
直角三角形の相似条件は「直角以外の角度一つが等しい」「対応する2辺の比が等しい」の2つです。この相似条件を用いる証明問題も解説します。 静止画 e1soj1jpg 600×400、 1195KB 中学数学 ⇒ 相似と比(中学3年) ⇒ 三角形の相似条件 三辺の比相当 三角46探索三角形相似的条件 一、选择题 1下列命题错误的是()毛 a两角对应相等的两个三角形相似;b两边对应成比例的两个三角形相似 c两边对应成比例且夹角相等的两个三角形相似;d三边对应成比例的两个三角形相似 2下面关于直角三角形的相似叙述错误的是() a有一锐角对应相等的两个直角三角形 0048 直角三角形相似的判定 a a′ b 0048 ∟ c b′ c′ 两个直角三角形,满足什么条件,两直角 三角形相似? 1有一个锐角相等的两 个直角三角形相似; 2两直角边对应成比例 的两直角三角形相似 0048 斜边和一条直角边分别对 应相等的两个直角三角形 全等。




超级精品 初中数学几何模型



相似三角形的判定 相似ppt 第3课时 第一ppt
三角形 相似条件 三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分か三角形の相似 直角三角形の合同条件を使った証明問題の解き方 現役塾講師の 中2数学図形の証明問題を攻略できる7つのコツ Qikeru学びこんにちは、ウチダです。 今日は、中学3年生で習う 「三角形の相似条件」 について、まずは図形の相似を解説し、次に三角形の相似条件が $3$ つである理由を明らかにしていきます。 また記事の後半では、狙われやすい証明問題をいくつか用意しましたので、ぜひチャレンジしてみて下さい。 三角形の相似条件 相似は図形問題の中でもずば抜けて出題されやすいとても重要なものです。 よって、相似条件も絶対に覚えなければいけませんが、特に「2組の角がそれぞれ等しい」という条件は相似条件の中でも99%出やすいです。 2組の等しい角を



直角三角形 图片欣赏中心 急不急图文 Jpjww Com



这道初三几何题难倒不少人 解题关键是证明相似和构造直角三角形 文化资讯 娱乐新闻网
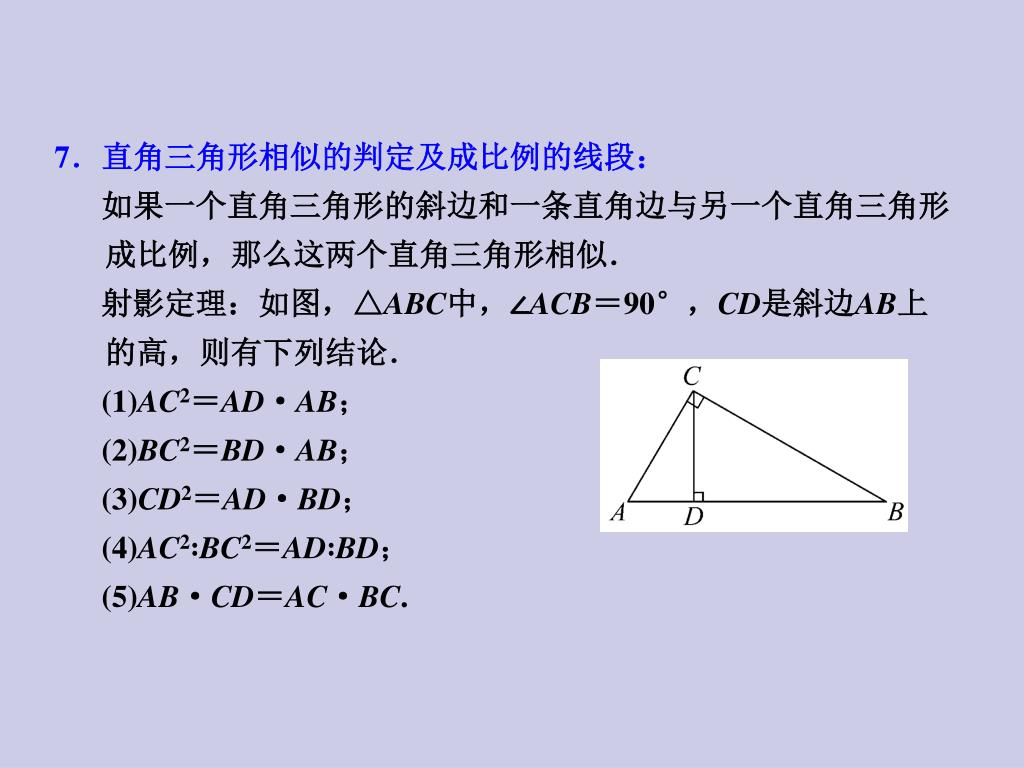
三角形 A B C と H B A はいずれも直角三角形です。 そして、 ∠ B を共通に持ちます。 よって、これらの三角形は 直角以外の角度一つが等しい直角三角形 なので、直角三角形の相似条件1より相似であることが証明されました。 应该可以。 县根据两直角三角形的斜边和直角边求出另一直角边的长度。 因为两三角形的斜边和一条直角边成比例,所以所求出的另一直角边也一定成比例。 两直角边成比例,其夹角(直角)也相等,则两直角三角形相似 全部 我需要的不是2直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似,并且分成的两个直角三角形也相似。 编辑本段三角形相似的判定定理推论 推论一:顶角或底角相等的两个等腰三角形相似。 推论二:腰和底对应成比例的两个等腰三角形相似。 推论三:有




若直角三角形中斜边的长为13一条直角边长为5则这个 初中二年级下学期数学
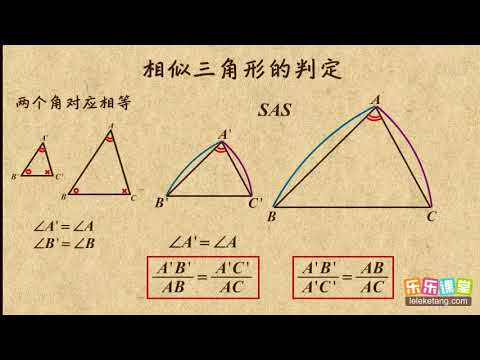



03相似三角形的判定图形的相似初中数学初三 Youtube
次に説明する 2つの三角形が相似といえる3つの条件 は非常に重要なものなので覚えておきましょう。 三角形の相似が成り立つ条件①:2組の角が等しい 2つの三角形の 2組の角が等しければ相似 であるといえます。三角形の相似条件 「 三角形の合同条件 」は、「 形 」も「 大きさ 」も同じというための条件。在什么条件下图形是等腰三角形、直角三角形、四边形是菱形、梯形等; 探索两个三角形满足什么条件相似等; 探究线段之间的位置关系等; 探索面积之间满足一定关系求x的值等和直线(圆)与圆的相切时求自变量的值等。



初三数学中一道求面积的题难倒众人 运用这个方法则可瞬间解决



非平凡的镜像相似性 科普之友
三角形の相似条件、記号、相似比・面積比、証明問題 21年2月19日 この記事では、「相似」の意味や記号、三角形の相似条件、相似比と面積比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね母子型相似三角形模型 典型 母子型相似三角形 知识要点 一、直角三角形相似 1、直角三角形被斜边上的高分成两个直角三角形和原三角形相似。 2、如果一个直角三角形的斜边和一条直角边 江苏省丹徒区高资镇石马中学苏科版九年级数学下册学案(无答案):64 探索三角形相似的条件(4) 19 江苏 镇江市丹徒区石马中学 学案/导学案 下载 zhangd13 加入资




觀念 直角三角形的母子相似性質 Youtube



70以上直角三角形相似条件 ニーアオートマタ壁紙
两三角形相似的条件 作业帮 _____ 三种判别方法1有两个角对应相等;2两个边对应成比例,夹角相等;3三边对应成比例 证明图形相似的条件 _____ sss aaa sas aas ssa 平行于第三边的直线交另两条线的两三角形相似 性质中三角形全等是条件,结论是对应角、对应边相等 直角三角形の合同条件には、以下の つがあります。 条件①斜辺と 1 つの鋭角がそれぞれ等しい つの角が であることから、斜辺の長さおよび つの鋭角が等しいことが示せれば、 残りの 角も自ずと定まります 。 問2 下の図の三角形を、合同な三角形の組に分けなさい。また、そのとき使った合同条件をいいなさい。 3㎝ 3㎝ 3㎝ 3㎝ 5㎝ 5㎝ 5㎝ 5㎝ 5㎝ 5㎝ 70° ° ア イ ウ エ オ カ※ 特に,直角三角形では相似条件の③により 直角以外のもう一つの角が等しければ相似ということになります。
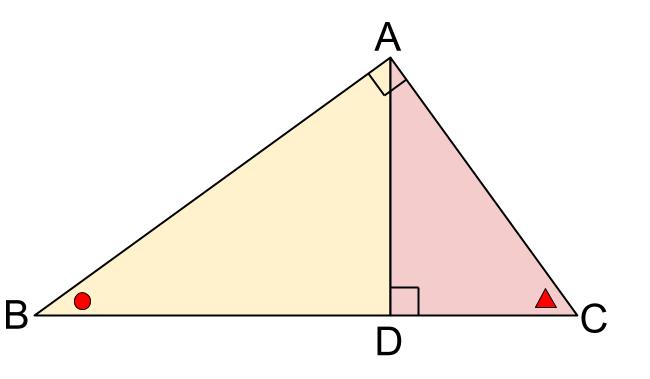



中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su



三角形三种不同的画法 图片欣赏中心 急不急图文 Jpjww Com
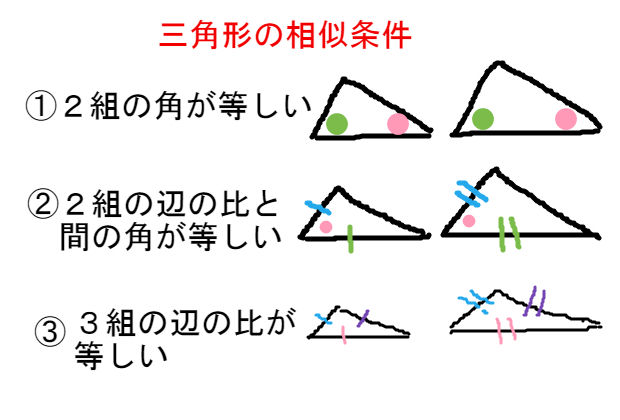
三角形の相似条件 3組の辺の比 がそれぞれ等しい 2組の辺の比 と その間の角 がそれぞれ等しい 2組の角 がそれぞれ等しい 合同条件と似ているのがわかるかと思います。 1番目と2番目は「辺」が「辺の比」になり、3番目は「辺の長さに関する条件」が
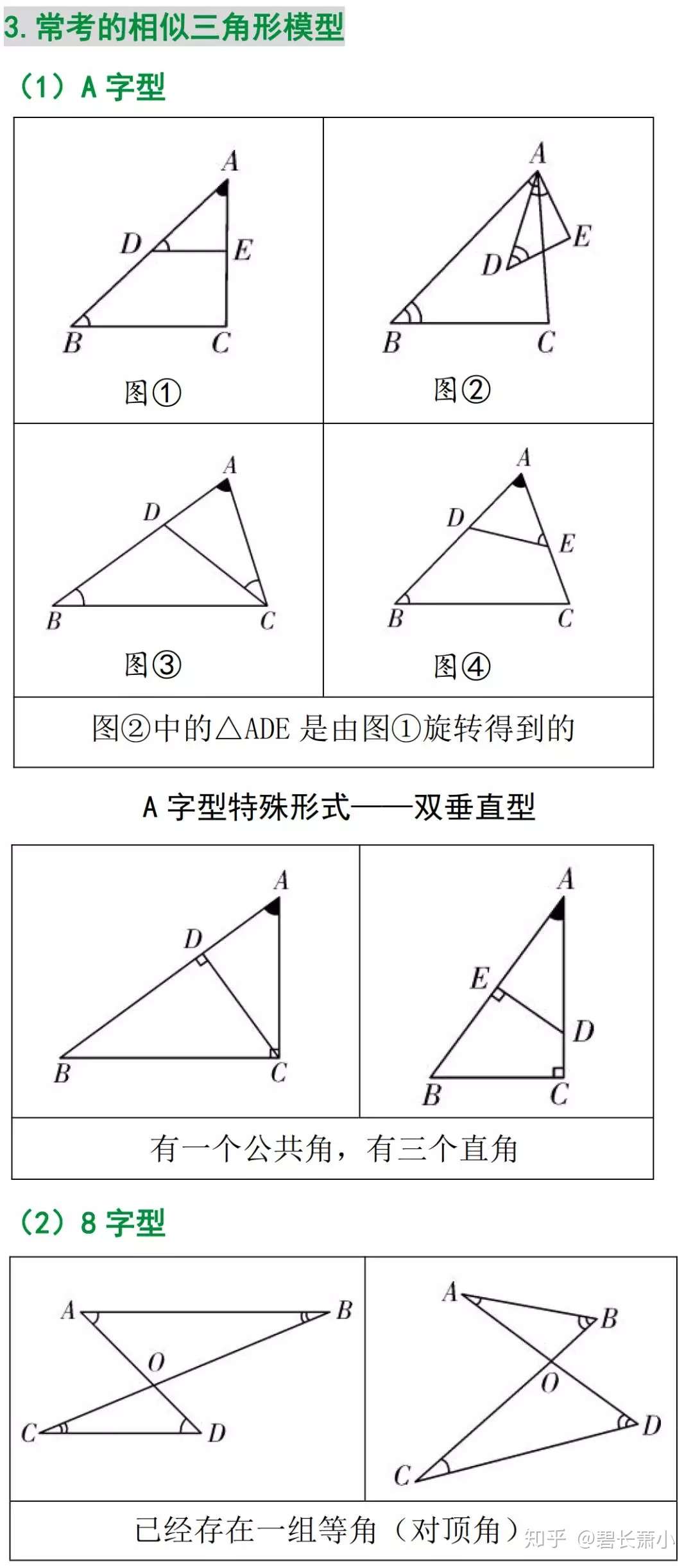



中考数学 相似三角形有关的证明与计算 知乎




相似三角形定理和性质




相似条件 合同条件 中学生 数学のノート Clear




K字型 母子型相似模型下载 Word模板 爱问共享资料




学习 我一直在路上 简书




相似三角形复习练习题 Doc 文档分享网



直角三角形の相似条件 具体例で学ぶ数学



三角形の相似 合同条件 優技録



直角三角形角度 西瓜视频搜索



探索三角形相似的条件 图形的相似ppt 第2课时 第一ppt



课程信息 本讲教育信息 一 教学内容 相似三角形和三角形相似的条件 1 了解相似三角形 相似比的含义 2 掌握两个三角形相似的判断条件 并能够运用三角形相似的判断方法解决一些简单的问题 二 知识要点 1 相似三角形 1 相似三角形 对应角



相似 直角三角形




求等腰三角形顶点的坐标




27 2 3 相似三角形应用举例 初中电子课本




思维导图 全面解析初中数学 三角形的性质定理及判定 雪花新闻




直角三角形全等判定 提高 巩固练习




求等腰三角形顶点的坐标
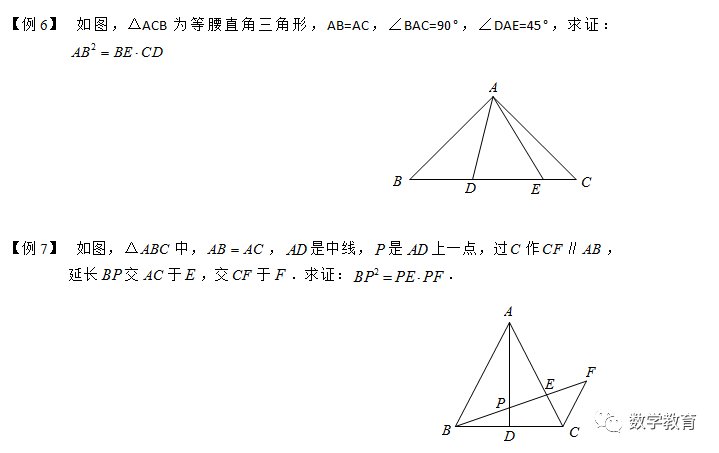



怎么证明两个三角形相似




相似三角形旋转模型 相似三角形经典模型 旋转相似经典例题



4 4两个三角形相似的判定导学案 图片欣赏中心 急不急图文 Jpjww Com



相似三角形定理 尚书坊
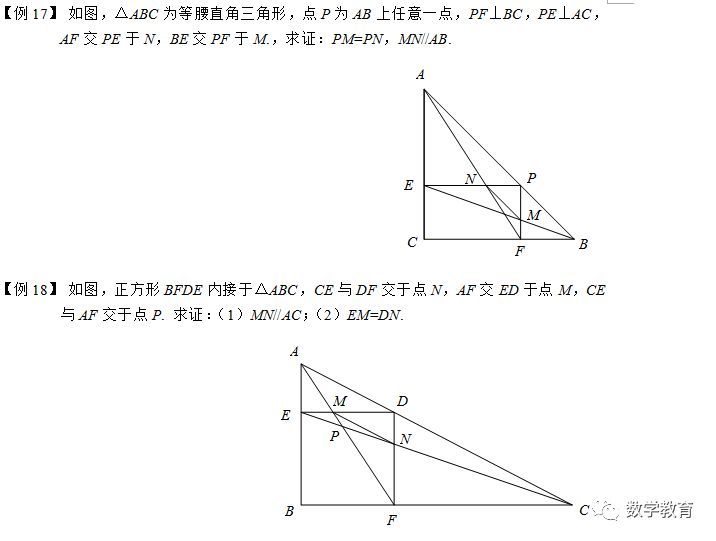



怎么证明两个三角形相似




直角三角形之母子相似性質 Live 多媒體數學觀念典online



1
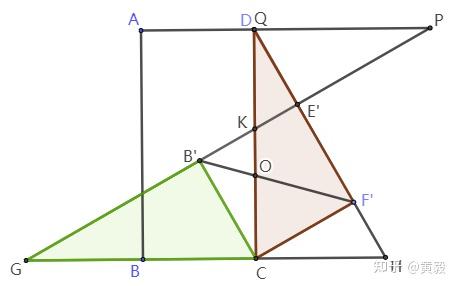



旋转背景下的面积比值问题 21年宜昌市中考数学第23题 知乎




直角三角形全等判定 提高 巩固练习
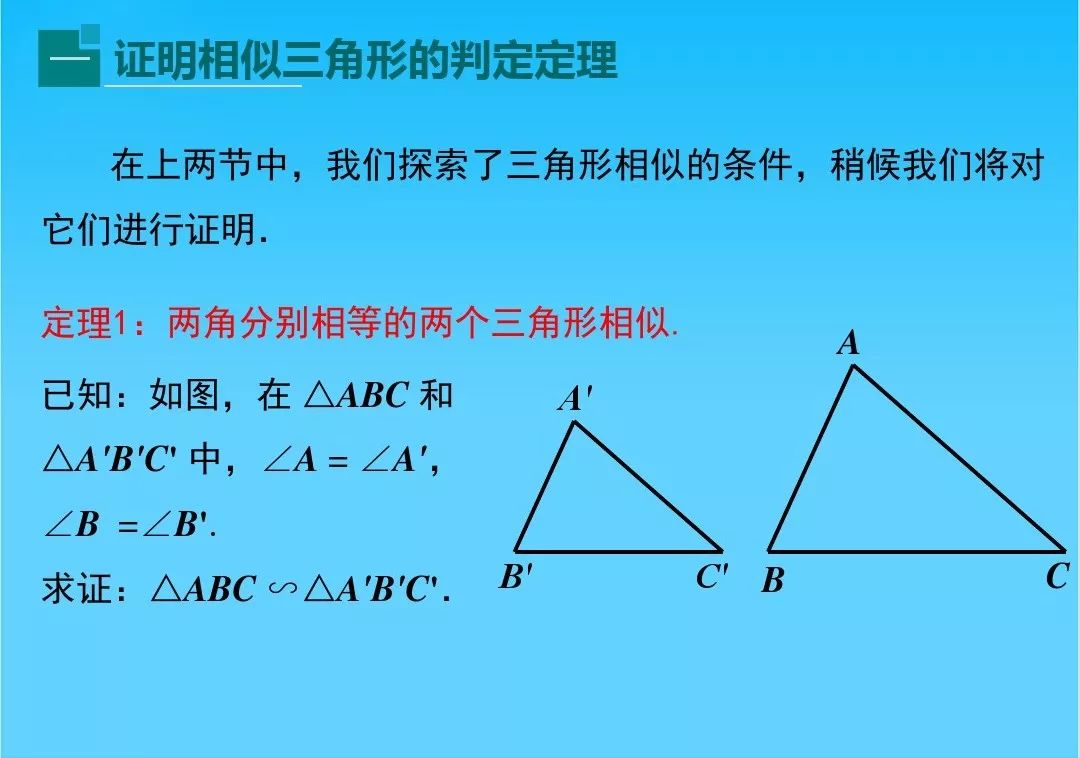



多重判定系数怎么求 北师大版九上数学4 5 相似三角形判定定理的证明知识点精讲 Yu Demon321 Mkq的博客 程序员宅基地



三相似三角形的判定及性质 人教版高中选修4 1数学电子课本 数九网



1
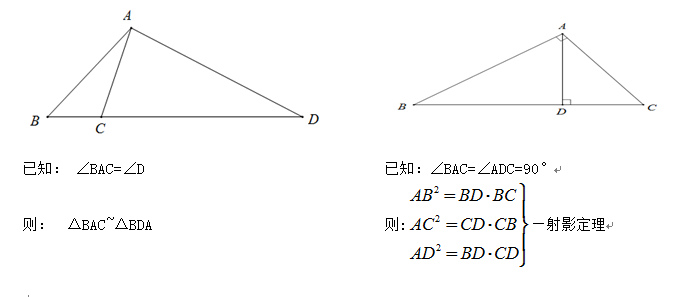



初中数学知识点相似三角形的判定及性质




Math 相似 直角三角形 正三角形と相似 働きアリ



Math 相似 直角三角形 正三角形と相似 働きアリ



三角形的相似条件 数学作业 解题作业帮




教学反思 为什么判定相似不能用 边边角 三角形 直角 锐角 钝角 网易订阅




相似三角形的性质及其判定定理是什么 星火网校



三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト




初三相似三角形提高拓展专题练习附答案 豆知网



相似三角形定理 学习岛



1



直角三角形之母子相似性質 Live 多媒體數學觀念典online
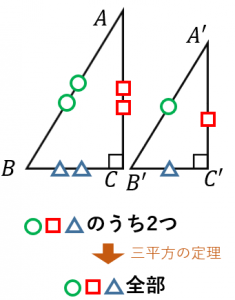



直角三角形の相似条件 具体例で学ぶ数学



Ppt 图形的相似powerpoint Presentation Free Download Id




例題 相似三角形面積比 直角三角形 Youtube




老师熬夜整理 初中数学最全几何模型大汇总 学生大呼 过瘾




C 直角空心三角形 九年级上册相似三角形填空题50题冲刺 图片版 附答案 Weixin 的博客 程序员宅基地 程序员宅基地




第24讲相似三角形考点知识精讲中考典例精析举一反三考点训练 Ppt Download




多重判定系数怎么求 北师大版九上数学4 5 相似三角形判定定理的证明知识点精讲 Yu Demon321 Mkq的博客 程序员宅基地
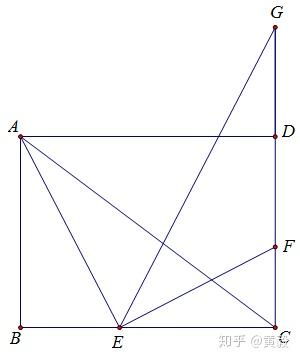



利用特殊直角三角形简化相似三角形存在性问题 知乎




什么叫相似三角形




三角形相似的判定条件



在初中数学教材 人教版 中 给出四种任意三角形的判定方法和一种直角 一家家教育网




三角形の相似条件



1000以上直角三角形相似条件 ニスヌーピー壁紙
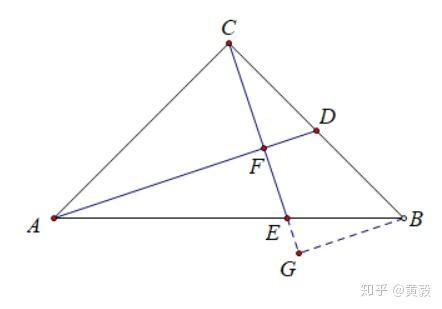



突破难点的关键是构造直角三角形相似基本型 知乎



直角三角形 信息图文欣赏 信息村 K0w0m Com




直角三角形邊長角度三角形 Dwfne
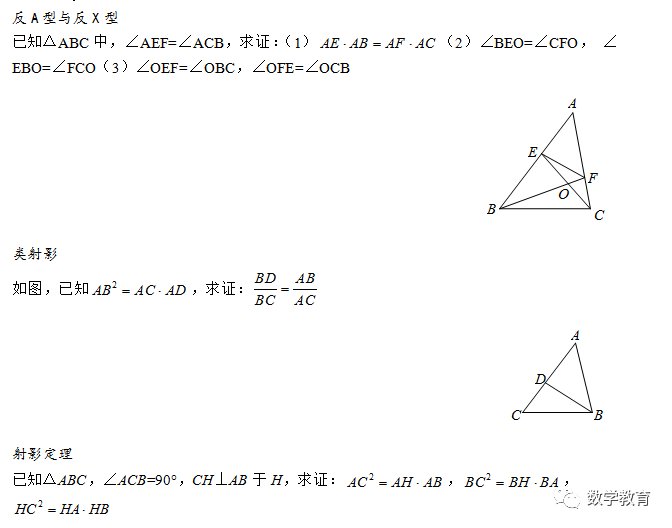



怎么证明两个三角形相似




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく




探索三角形相似的条件 图形的相似ppt课件 Ppt课件下载 人人ppt
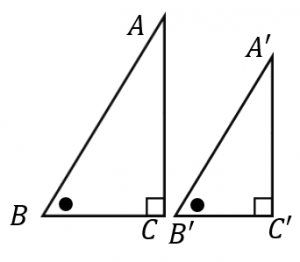



直角三角形の相似条件 具体例で学ぶ数学
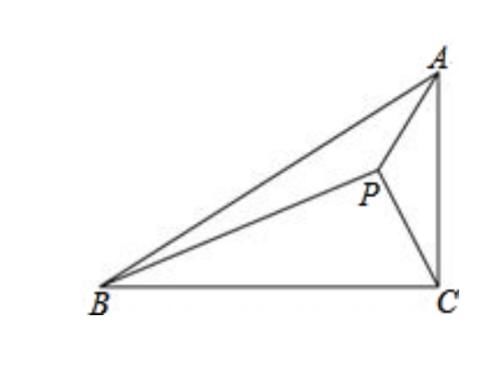



证明直角三角形相似的条件



印度数学竞赛题 考查勾股定理和相似三角形 学霸直言没中考题难 教育资讯 早游戏



1




相似三角形的判定



等腰直角三角形中的共斜边问题 一 方法




超级精品 初中数学几何模型




数学 相似三角形 Hl判定 的证明 哔哩哔哩




老师熬夜整理 初中数学最全几何模型大汇总 学生大呼 过瘾




探索三角形相似的条件 图形的相似ppt课件3 Ppt课件下载 人人ppt




Z2qcyzrfbnzolm



27 2 相似三角形 人教版九年级下册数学电子课本 数九网



三角形问题判定表图片 信息评鉴中心 酷米资讯 Kumizx Com
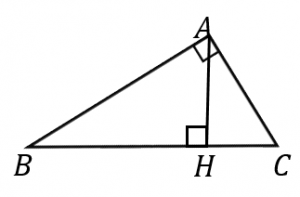



直角三角形の相似条件 具体例で学ぶ数学



Ppt 相似三角形复习课powerpoint Presentation Free Download Id



直角三角形三边长度 图片欣赏中心 急不急图文 Jpjww Com



60度直角三角形边长 西瓜视频搜索
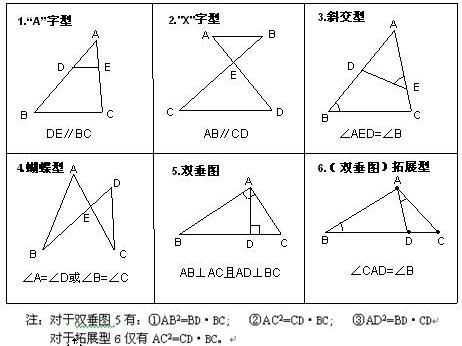



相似形 搜狗百科




九年级数学三角形相似的判定 Ppt课件




數學一點也不無聊 課堂有趣事 直角三角形母子相似性質




三角形 相似與全等證明
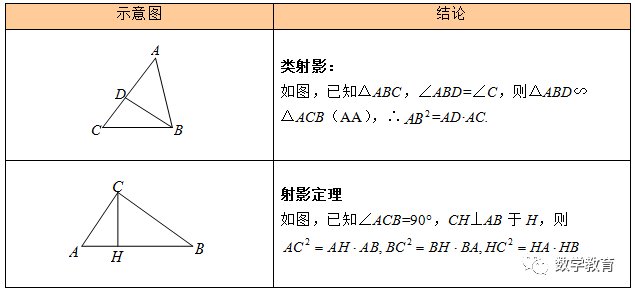



怎么证明两个三角形相似




中考数学相似三角形专题复习 知识点总结 解题技巧 中考例题 每日头条
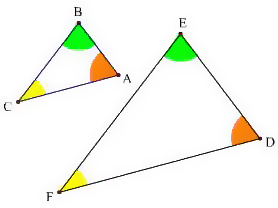



相似三角形 维基百科 自由的百科全书



70以上直角三角形相似条件 ニーアオートマタ壁紙



学霸们 来看看这几道小升初后的入学分班数学压轴几何题 爱子网
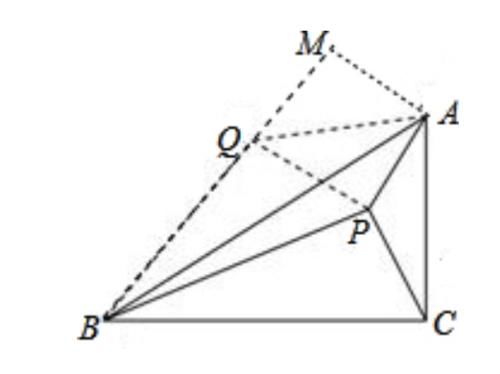



证明直角三角形相似的条件




數學一點也不無聊 課堂有趣事 直角三角形母子相似性質




初中数学相似三角形定理知识点总结 快资讯



23 3 2相似三角形的判定1课时作业 文章阅读中心 急不急图文 Jpjww Com




相似三角形 相似ppt课件2 Ppt课件下载 人人ppt



0 件のコメント:
コメントを投稿